Systemanalyse - Atlas optimization

Optimal control: Systemanalyse

Problemstellung

Die Steuerung zeitabhängiger Systeme ist ein schwieriges Unterfangen, dessen Erfolg nicht unter allen Umständen garantiert werden kann. Manche Systeme sind instrinsisch instabil und geraten ausser Kontrolle unabhängig vom Steuerungsinput.

Andere Systeme stellen dem entscheidungstreffenden Algorithmus nicht genug Informationen zur Verfügung, um sinnvolle Steuerungsanweisungen abzuleiten.

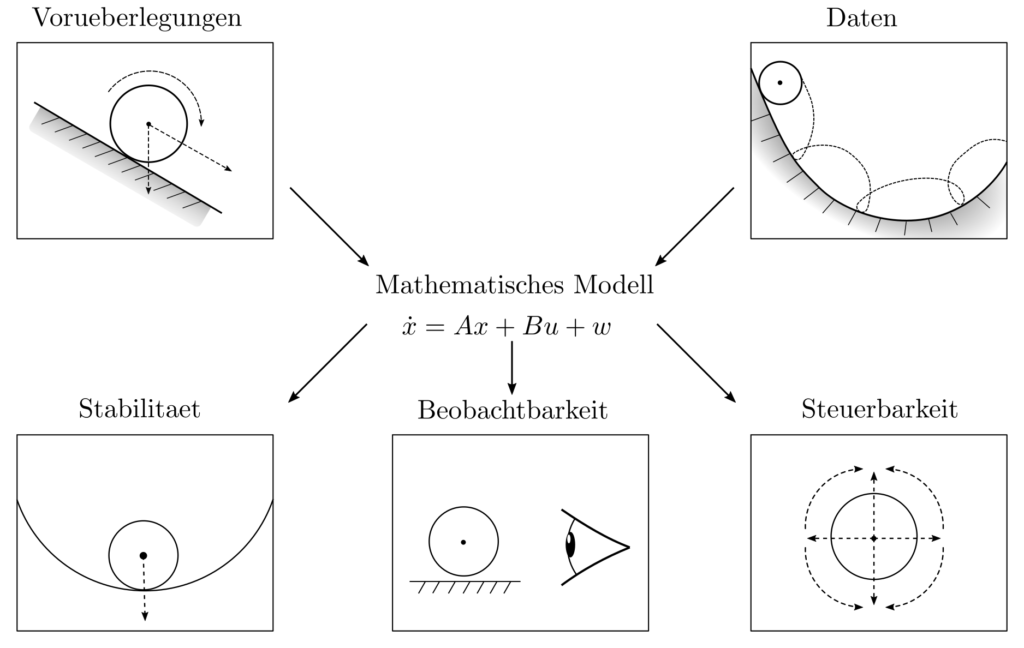
Es ist zur Abschätzung des Steuerungserfolges notwendig, zentrale Systemcharakteristiken wie Stabilität, Steuerbarkeit, und Beobachtbarkeit zu untersuchen. Erst dann können die potentiellen Probleme bei der Steuerung des Systemes identifiziert und Gültigkeitsgrenzen sowie Erfolgsgarantien ausgesprochen werden. In der Praxis wird diese theoretische Systemanalyse noch erschwert durch unbekannte dynamische Zusammenhänge, die vor jeglicher weiterer Untersuchung aus Beobachtungsdaten und Vorüberlegungen abzuleiten sind.

Beispielhaftes Systemverhalten

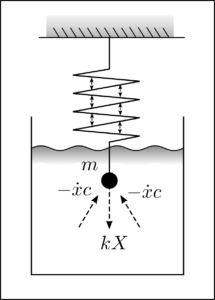
Sei ein dynamisches System definiert durch die Gleichung eines gedämpften harmonische Oszillators.

$$ \ddot{x} = \frac{c}{m} \dot{x} + \frac{k}{m}x=0$$

Die Gleichung beschreibt Position $x$, Geschwindigkeit $\dot{x}$, und Beschleunigung $\ddot{x}$ einer elastisch schwingenden Masse $m$ in einer typischerweise viskosen Flüssigkeit mit Dämpfungskoeffizient $c$. Der Parameter $k$ ist die Federkonstante, welche Auslenkung und Beschleunigung koppelt.

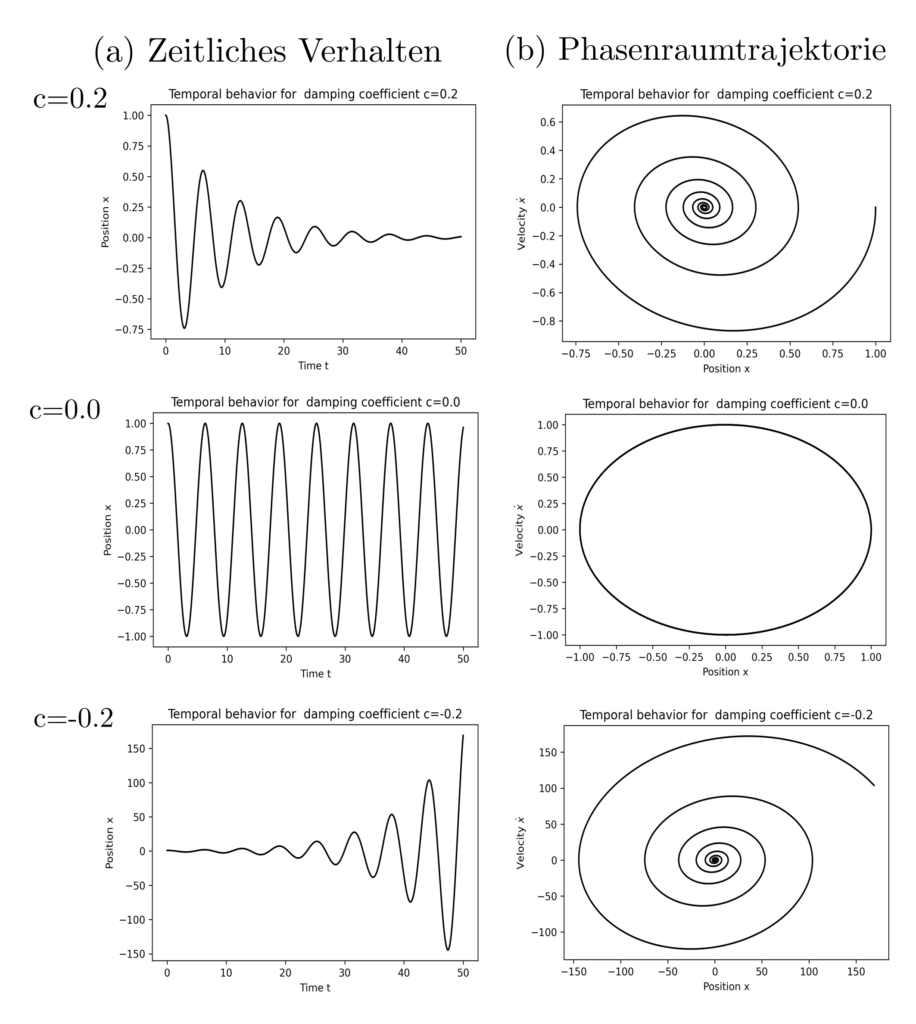
Beispielhafte Systemanalyse

Die qualitativen Unterschiede im Systemverhalten lassen sich erklären und direkt prädizieren. Die Differentialgleichung für den gedämpften Oszillator lässt sich auch schreiben als

$$ v=\begin{bmatrix} v_1 \\ v_2 \end{bmatrix}= \begin{bmatrix} x \\ \dot{x}\end{bmatrix} ~~~ \dot{v} = \begin{bmatrix} \dot{x}\\ \ddot{x}\end{bmatrix} = \begin{bmatrix} v_2 \\ -(c/m)v_2 -(k/m) v_1\end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -(k/m) & -(c/m)\end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = Av$$

wobei $\dot{v}$ die zeitliche Ableitung von $v$ ist. Aus der Gleichung $\dot{v}=Av$ lassen sich direkt problematische Konstellationen Ableiten: Gäbe es z.B. ein $v_0$ mit $Av_0=\lambda v_0$ und $\lambda > 0$, dann gälte für $v_0=v(0)$ gerade

\begin{align} ~~~~~~\dot{v}(0) & = \lambda v(0) \\ \Rightarrow v(\Delta t) & \approx (1+\lambda \Delta t)v(0) \\ \Rightarrow v(2\Delta t) &\approx (1+\lambda \Delta t)v(\Delta t) \\ & \vdots \\ \Rightarrow v(n\Delta t) &\approx (1+\lambda \Delta t) v((n‑1)\Delta t) \end{align}

sodass der Zustandsvektor $v(t)=[x(t), \dot{x}(t)]$ mit jedem Zeitschritt etwas grösser wird und somit ins Unendliche wächst. Gilt hingegen für jedes $v\in \mathbb{R}^2$, dass $v$ durch $v+\Delta t A v$ betragsmässig verkleinert wird, dann konvergiert das System für alle Anfangszustände gegen $[0,0]$ und stabilisiert sich selbst. Die Frage nach der Stabilität ist demnach primär eine Frage nach den Vorzeichen von Eigenwerten der Matrix $A$; sind alle negativ ist das System stabil [1, p. 24].

Äquivalent zu diesem Kriterium ist die lineare (Lyapunov) Matrixungleichung [2]

$$ P \succeq 0 ~~~~A^TP+PA \preceq 0 ‚$$

die nur im Falle eines stabilen Systemes erfüllbar ist. Neben Steuerbarkeit und Beobachtbarkeit gibt es weitere Eigenschaften wie etwa Stabilisierbarkeit und Detektierbarkeit, deren Vorhandensein die Existenz eines optimalen konstanten Feedbackloops $u=Kx$ garantiert.

Systeme mit Steuersignal

Kann auf ein System aktiv eingewirkt werden mit dem Steuersignal $u$, dann ist die Situation komplizierter. Es muss untersucht werden, ob ein das System stabilisierendes $p$-dimensionales Steuersignal $u$ existiert und ob es aus möglicherweise defizienten Beobachtungen abgeleitet werden kann.

Die rechtseitige Skizze illustriert die Zusammenhänge: Ein Zustand $v$ wird inkomplett beobachtet. Dies führt zum Messwert $y$, welcher zu einem Steuersignal weiterverarbeitet werden muss. Zustand, Steuersignal, und Zustandsänderung sind über die Matrizen $A,B$ miteinander gekoppelt.

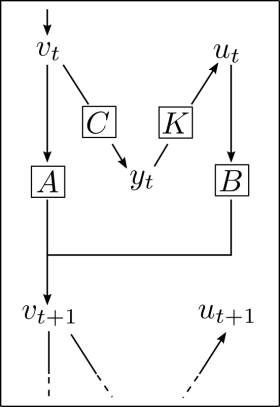
Mathematisch kompakter formuliert werden die obigen Zusammenhänge als das lineare System $(A, B, C)$

\begin{align} \dot{v} & = Av(t) + B u(t) ~~~~~&&v\in \mathbb{R}^n ~~ A\in \mathbb{R}^{n\times n}, ~~B\in \mathbb{R}^{n\times p} \\ y(t)&=Cv(t) && y\in \mathbb{R}^m ~~ C \in \mathbb{R}^{m\times n} \end{align}

mit den Matrizen $A, B, C $. Es vermittelt zwischen Zustandsvektoren, Steuersignalen und Beobachtungen.

Steuerbarkeit und Beobachtbarkeit

Das System kann mithilfe von linearen Matrixungleichungen auf seine Steuerbarkeit und die Hinlänglichkeit der Beobachtungen $y$ für die Steuerung untersucht werden. Es gilt [2]

Entweder das System $(A,B,I)$ ist steuerbar oder es existiert eine symmetrische Matrix $P\neq 0$, sodass $$ AP+PA^T\preceq 0 ~~PB=0.$$
Entweder das System $ ( A, B, C)$ ist beobachtbar oder es existiert eine symmetrische Matrix $P\neq 0$, sodass $$ AP+PA^T \preceq C^T=0.$$

So können aus der Lösbarkeit von semidefiniten Programmen globale Systemeigenschaften abgeleitet werden.

Optimale Steuersignale

Für ein System der Form $\dot{x}=Ax+Bu$ mit direkt beobachtbaren Zuständen $x$ können die Steuersignale direkt aus den Zustandsbeobachtungen abgeleitet werden. Es sei die quadratische Kostenfunktion $\int_0^{\infty}u(t)^TRu(t)+x(t)^TQx(t) dt$ zu minimieren. Sie besteht aus Kosten für die Aufwendung des Steuersignales $u(t)$ und den Kosten für die Abweichung des Zustandes $x(t)$ vom gewünschten stabilen Zustand $x=0$.

Es gilt dann $u=Kx$ mit $K$ einer Matrix, welche Zustände auf Steuersignale abbildet und die folgenden Matrixgleichungen erfüllt [3, pp. 35–40].

\begin{align} K&=-R^{-1}B^TP \\ 0 & = A^T P + PA — PBR^{-1}B^TP+Q \\ P& \succeq 0\end{align}

Die Gleichung für die Matrix $P$ heisst algebraische Riccati Gleichung und ist quadratisch in $P$. Die Suche nach einem das System optimal steuernden $K=-R^{-1}B^TP$ kann formuliert werden als semidefinites Optimierungsproblem in der Matrixvariable $P$ [4, p. 9].

$$ \begin{align} \min_P ~~~& -\operatorname{tr} P \\ \text{s.t.} ~~~&\begin{bmatrix} A^TP+PA+Q & PB \\ B^TP & R\end{bmatrix} \succeq 0 \\ ~~~& P \text{ symmetrisch} \end{align}$$

Anwendung

Es sei der gedämpfte harmonische Oszillator nun teilweise steuerbar mit Steuersignal $u$ gemäss der Gleichung

\begin{align} \dot{x}&=Ax + Bu \\ A&=\begin{bmatrix} 0 & 1 \\ ‑1 & ‑0.2\end{bmatrix} ~~~~~ B =\begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{align}

wobei $ x=[\text{ Position , Geschwindigkeit}]$. Dann gilt unter den Nebenbedingungen $PB=0$ und $A^T+PA\preceq 0$ mit $P$ symmetrisch gerade $\max (\operatorname{tr} P )=\min( \operatorname{tr} P)$ mit dem optimalen $P^*=0$ und das System ist steuerbar. Gleichzeitig gilt $PC^T=0$ und $AP+PA^T\preceq 0$ mit $P$ symmetrisch und $\max (\operatorname{tr} P )=\min( \operatorname{tr} P)$ mit $P^*=0$ und das System ist beobachtbar. Die Lösung des semidefiniten Programmes

$$ \begin{align} \min_P ~~~& -\operatorname{tr} P \\ \text{s.t.}
~~~&\begin{bmatrix} A^TP+PA+I & PB \\ B^TP & 1\end{bmatrix} \succeq 0 \\ ~~~& P \text{ symmetrisch} \end{align}$$

ist $P^*=[1.73, 0.414; 0.414, 1.167]$ mit $K=-B^TP=[-0.414, — 1.167]$. Mit dem Steuersignal $u^*=Kx$ wird das Kostenfunktional $\int_{0}^{\infty} x^2(t)+\dot{x}(t)^2 + u^2(t) dt$ minimal.

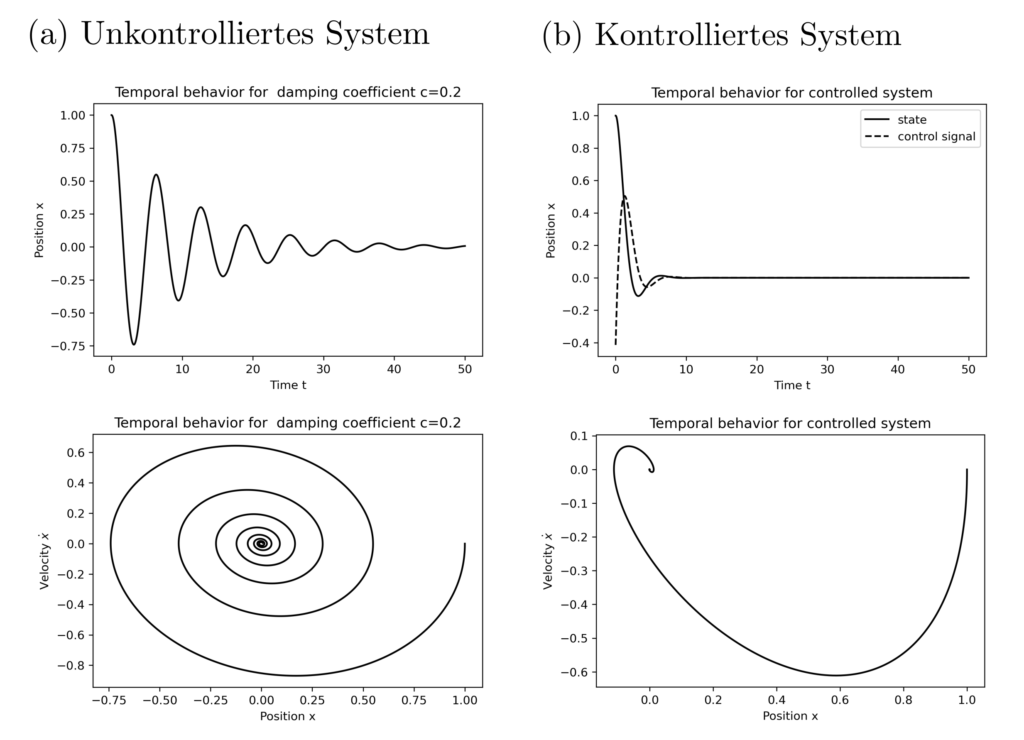
Praktisches

Sind die Matrizen $A$ und $B$ zeitabhängig, dann ist auch die Feedbackmatrix $K$ zeitabhängig und $P$ erfüllt eine Differentialgleichung. Sind die Zusammenhänge zwischen $x, u, $ und $\dot{x}$ nichtlinear, so kann eine optimale Steuerung unter Umständen trotzdem erreicht werden. Dazu ist zu untersuchen, ob die Auswirkungen der Nichtlinearität begrenzbar sind durch lineare Ungleichungen. Dasselbe wie für Nichtlinearitäten gilt auch für Zufallseffekte.

In der Praxis ist die Modellierung eines Echtweltphänomenes als lineares System $\dot{x}=Ax+Bu$ ebendalls herausfordernd. Dazu sind oft höherdimensionale Einbettungen und Linearisierungen notwendig und die Modellierung kann trotz aller Tricks scheitern.

Durch die Komplexität der echten Welt ist Nichtlinearität ein häufiger verkomplizierender Faktor, der Steuerbarkeitsgarantien aufweicht und die Einführung experimenteller Methoden wie Reinforcement learning erfordert. Lineare Modelle und deren Analyse sind nichtsdestotrotz nützliche Werkzeuge zur Untersuchung vor allem technischer und von Menschenhand designter Prozesse.

Code & Quellen

Beispielcode: OC_harmonic_oscillator_1.py , OC_harmonic_oscillator_2.py in unserem Tutorialfolder.

[1] Dym, C. L. (2002). Stability Theory and Its Applications to Structural Mechanics. New York: Dover Publications.

[2] Balakrishnan, V., & Vandenberghe, L. (2003). Semidefinite programming duality and linear time-invariant systems. IEEE Transactions on Automatic Control, 48,(1), 30–41.

[3] Anderson, B. D. O., & Moore, J. B. (2007). Optimal Control: Linear Quadratic Methods. New York: Courier Corporation.

[4] Yao, D. D., Zhang, S., & Zhou, X. Y. (2001). Stochastic Linear-Quadratic Control via Semidefinite programming. SIAM Journal on Control and Optimization, 40, (3), 801–823.