Numerik und solver - Atlas optimization

Theorie: Numerik und solver

Definition

Die Numerik beschöftigt sich mit der algorithmischen rechnergestützten Lösung konkreter Probleme der angewandten Mathematik. Die in der Numerik entworfenen Algorithmen führen ausgehend von standardisierten Problemformulierungen in endlich vielen Schritten zu einer approximativen Lösung.

Die Implementation eines Algorithmus zur Lösung von Optimierungsproblemen in Form von ausführbarem Programmcode wird solver genannt.

Unstrukturierte Ansätze
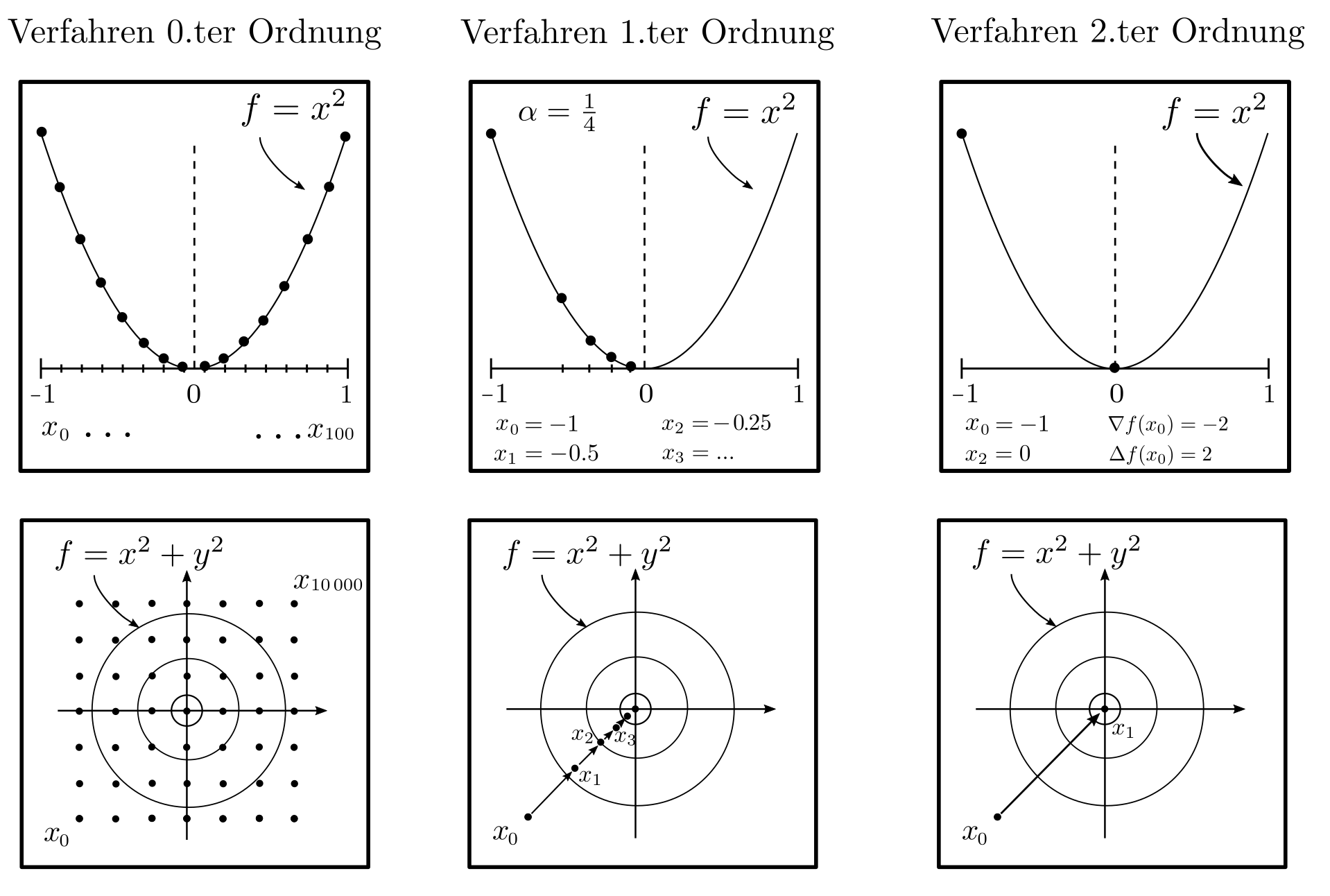
0‑ter Ordnung

Lösungsalgorithmen für Probleme der Form $\min_x f(x) : x \in D$ sollen demnach eine Folge $x_1, …, x_m \in D$ von Punkten generieren, sodass $f(x_m) — f(x^*) \le \epsilon$ wobei $x^*$ das wahre Optimum und $\epsilon$ eine kleine positive Zahl ist, welche die Mindestgenauigkeit der approximativen Lösung $x_m$ vorschreibt.

Der Lösungsalgorithmus benötigt dazu Zugriff auf die Zielfunktion $f$ und die Nebenbedingungen $D$. Im allgemeinsten Fall sind keine globalen strukturellen Informationen bekannt und es können lediglich konkrete Funktionswerte $f(x_1), …, f(x_m)$ bereitgestellt werden. Mit diesen spärlichen Informationen benötigt man für eine approximative Lösung $x_m$ mit $f(x_m)-f(x^*)\le \epsilon$ mindestens [1, p. 11]

$$m \ge \left(\frac{L}{2 \epsilon} ‑1 \right)^n $$

Optimierungsschritte wobei $n$ die Anzahl an dimensionen der Optimierungsvariable $x$ und $L$ eine obere Schranke für die Ableitung von $f$ ist. Die Gleichung zeigt, dass die Auffindung des optimalen $x^*$ durch systematisches Ausprobieren verschiedener $x$ ein hoffnungsloses Unterfangen ist: Schon für ein $x$ mit 10 Komponenten bräuchte eine handelsüblicher Computer mehrere Millionen Jahre und jede weitere Dimension verhundertfacht diese Zeitdauer [1, p. 12].

Unstrukturierte Ansätze
1‑ter und 2‑ter Ordnung

Sind neben dem Funktionswert $f$ an den Stellen $x_1, x_2, …$ auch der Vektor $\nabla f$ erster Ableitungen (=Gradient) und die Matrix $\Delta f$ zweiter Ableitungen (Hesse Matrix) verfügbar, so verringert sich die Anzahl benötigter Optimierungsschritte erheblich. Gradientenbasierte Verfahren

$$ x_{k+1} = x_k — \alpha \nabla f(x_k)~~~~~~k=0, 1, … ~~~~~\alpha >0 \text{ Schrittweite}$$

oder das Newton Verfahren

$$ x_{k+1}= x_k — \Delta f^{-1}\nabla f ~~~~~~k=0, 1, …$$

haben typischerweise lineare respektive quadratische Konvergenzraten [1, p. 37]. Das bedeutet, dass bei jedem Optimierungsschritt die Anzahl korrekter Dezimalstellen von $x_k$ um eine konstanten Betrag anwächst respektive sich verdoppelt. Das mit reinen Funktionswerten $f(x_1), f(x_2), … $ nur im Rahmen von Jahrmillionen lösbare Problem ist mit dem Newton Verfahren innerhalt weniger Millisekunden gelöst.

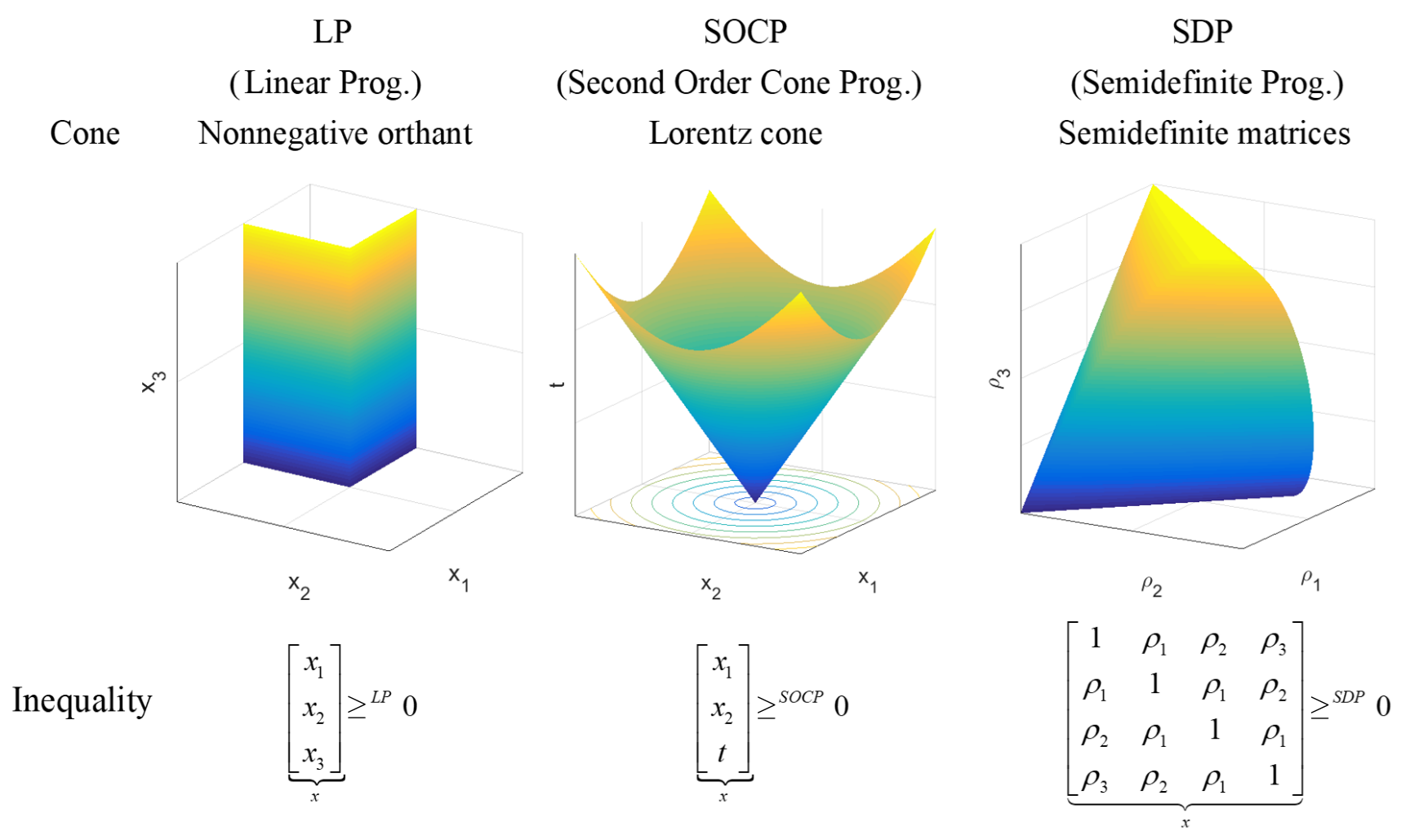
Kegelformulierungen

Je mehr also über die zu minimierende Funktion $f$ bekannt ist, desto schneller und zuverlässiger funktioniert die Optimierung. Es hat sich gezeigt, dass Informationen am besten in Form von Kegelbedingungen formuliert werden, sodass sämtliche Nichtlinearitäten in die Nebenbedingunge $x \in \mathcal{C}$ eingebettet werden, wobei $\mathcal{C}$ ein konvexer Kegel ist. Das Optimierungsproblem

\begin{align} \min_x & \langle x, c \rangle \\ \text{s.t.}& Ax = b \\ & x \in \mathcal{C} \end{align}

heisst Kegelprogramm und es konnte bewiesen werden, dass jedes konvexe Optimierungsproblem auf die obige Weise geschrieben werden kann [2, p. 60].

Lösungsverfahren

Die Klasse der Kegelprogramme ist demnach extrem expressiv. Ein weiterer Vorteil besteht darin, dass viele Kegelprogramme (unter anderem LP, QP, QCQP, SOCP, SDP) effizient gelöst werden können.

Dazu werden die Nebenbedingungen ersetzt durch logarithmische Barrierefunktionen, welche am Rand der zulässigen Menge gegen $ \infty$ streben und eine Folge von gegen das ursprüngliche Problem konvergierende Problemen ohne Nebenbedingungen wird gelöst. Die Anzahl von Rechenschritten in den resultierenden Verfahren hängt polynomial ab von der Dimension $n$ des Problemes und nicht mehr exponentiell [2, pp. 288–297].

Um zertifizierbar korrekte Lösungen zu generieren, werden ursprüngliches und duales Problem gleichzeitig gelöst, indem z.B. beim SDP das primal-duale Paar von Optimierungsproblemen

\begin{align} P ~~~ \min_X & \langle C,X\rangle_F \hspace{5cm}D ~~~ &\max_{y,S} & \langle b,y\rangle \\ \text{s.t.}& \langle A_k^T,X\rangle_F ~~~ k=1, …, m_1 &\text{s.t.}& \sum_{k=1}^{m_1} y_kA_k+S=C \\ & X\succeq 0 &&S \succeq 0 \end{align}

gleichzeitig gelöst wird. Dabei ist $\langle C,X\rangle_F= \sum_{k=1}^n\sum_{l=1}^n C_{kl}X_{kl}$. Die Minimierung des duality gaps $\langle C,X \rangle_F — \langle b,y\rangle=\langle X,S\rangle_F$ erfolgt dann mit Hilfe der am Rand der positiv semidefiniten Kegels gegen $\infty$ strebenden logarithmischen Barrierefunktion $-(\log \det X + \log \det S)=-\log \det (XS)\) führend auf das Optimierungsproblem [3, p. 13]

\begin{align} \min_{X,y,S} ~~~&\langle X, S\rangle_F — \mu \log \det(XS) \\ \text{s.t.} ~~~ & \langle A_k^T, X\rangle_F = b_k ~~~~~ k=1, … , m_1 \\ & \sum_{k=1}^{m_1} y_k A_k + S =C ~~~~~~~~.\end{align}

Dieses muss gelöst werden für eine abfallende Folge von Werten für $\mu$.

Algorithmus

Der konkrete Algorithmus vollzieht startend bei zulässigen primalen und dualen Variablen $X^0,S^0, y^0$ die folgenden Schritte bis zur Konvergenz [3, p. 118].

\begin{align} X_{k+1}&= X_k+\Delta X ~~~~~~ &&\Delta X= \mu_k S_K^{-1} ‑X_k — D\Delta S D \\ S_{k+1}&= S_K+\Delta && \Delta S=\sum_{k=1}^{m_1} \Delta y_k A_k \\ y_{k+1} &=y_k+\Delta y && \Delta y = Q^{-1} g\\ \mu_{k+1}&= \alpha \mu_k && 0<\alpha<1 \end{align}

Dabei sind $(Q)_{kl}=\langle D^T A_k^T, A_l D\rangle_F$, $ g= \mu \langle A_k^T, S_k^{-1}\rangle_f-b_k$ und $ D=S_k^{-1/2}(S_k^{1/2}XS_k^{1/2}(^{1/2}S_k^{-1/2}$. Wie aus den Gleichungen ersichtlich, müssen teils grosse Matrizen geformt und invertiert werden. Dies ist rechenintensiv aber von modernen Rechnern auch für tausende Variablen problemlos durchführbar. Da LP, QP, … nur spezielle Instanzen von SDP sind, ist der hier vorgestellte Optimierungsalgorithmus recht repräsentativ für das Vorgehen bei anderen Problemen als nur der semidefiniten Optimierung.

Solverliste

Neben einigen kommerziellen solvern gibt es auch öffentlich und konstenfrei zugängliche open source solver. Aus Performancegründen sind sie oft in der Programmiersprache C geschrieben. Besonders hervorheben möchten wir hier das Modellierungsframework CVXPY [4] für konvexe Optimierungsprobleme. Es ist zwar selber kein solver, bietet aber eine einheitliche Schnittstelle zu einer Vielzahl von solvern und eine automatisierte Grammatik zur Formulierung konvexer Probleme.

Solvername	Lizenz	Fähigkeiten	Organisation / Referenz
CVXOPT	GNU GPL	LP, QP, SOCP, SDP	Stanford CO Group
ECOS	GNU GPL‑3.0	SOCP	Embotech GmbH
GLPK	GNU GPL	LP, MILP	Moscow Aviation Institute
MDPtoolbox	BSD‑3	DP	Steven Cordwell
OR tools	Apache 2.0	LP, MILP	Google
SCIP	ZIB Academic License	LP, MILP, MINLP, CIP	Zuse Institut Berlin
scipy	BSD	LP, Blackbox	scipy python package
SCS	MIT	LP, SOCP, SDP, ECP, PCP	Stanford CO Group
CPlex	kommerziell	LP, QP, nonconvex QP, SOCP, MIQP, MISOCP	IBM
Gurobi	kommerziell	LP, MILP, QP, MIQP, QCP, MIQCP	Gurobi
Mosek	kommerziell	LP, QP, SOCP, SDP, MINLP	Mosek

LP = Linear Program, QP = Quadratic program, QCP = Quadratically constrainted program, SOCP = Second order cone program, SDP = Semidefinite program, ECP = Exponential cone program, PCP = Power cone program, CIP = Constraint integer program, DP = Dynamic programming, MI = Mixed integer, NLP = Nonlinear program

Quellen

[1] Nesterov, Y. (2013). Introductory Lectures on Convex Optimization: A Basic Course. Berlin Heidelberg: Springer Science & Business Media.

[2] Nesterov, Y., & Nemirovskii, A. (1994). Interior-point Polynomial Algorithms in Convex Programming. Philadelphia: SIAM.

[3] De Klerk, E. (2006). Aspects of Semidefinite Programming: Interior Point Algorithms and Selected Applications. Berlin Heidelberg: Springer Science & Business Media.

[4] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.