Optimierung | ML - Atlas optimization

Übersicht: Mathematische Optimierung

Definition

Mathematische Optimierung ist die Wissenschaft der bestmöglichen Entscheidung. Sie ist Teil der Schnittmenge von Mathematik, Software, und industrieller Anwendung und hat in den letzten Jahrzehnten aufgrund ihrer praktischen Relevanz und stetigen rechentechnischen Fortschrittes einen enormen Zulauf erfahren. Sie ist mittlerweile eines der aktuellsten und praxisrelevantesten Felder der modernen angewandten Mathematik und aus vielen Bereichen der Industrie nicht mehr wegzudenken.

Die mathematische Optimierung beschäftigt sich mit Optimierungsproblemen, d.h. Aufgaben der Form

\begin{align} \min_{x} ~~&f(x) \\ \text{s.t.} ~~& x \in D \end{align}

Dies ist zu lesen als die Suche nach einer Wahl für den Vektor \(x\), sodass die Funktion \(f(x)\) den kleinsten Wert annimmt und \(x\) bestimmte Eigenschaften \(D\) erfüllt.

Erklärung

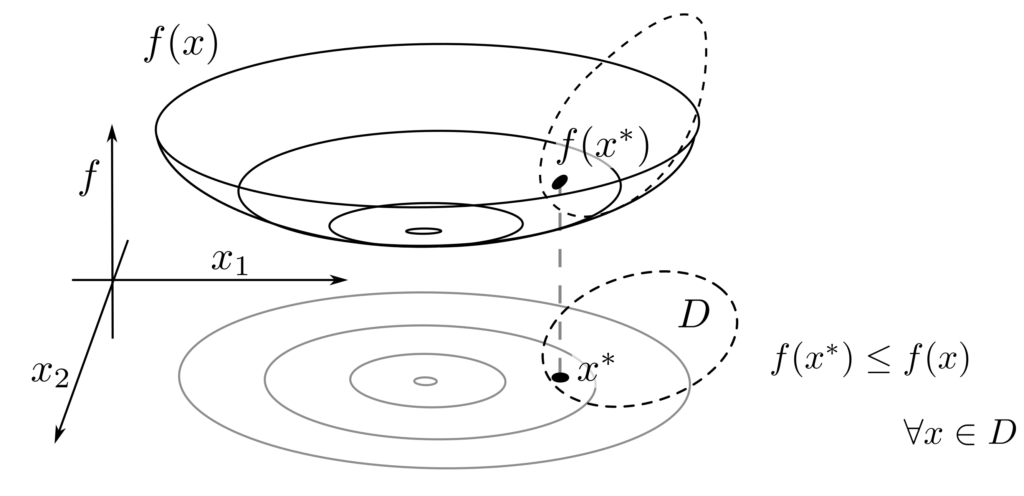
Die Funktion \(f(x)\) heisst Zielfunktion und gibt diejenige Grösse an, deren Wert verringert werden soll. Dies könnten Kosten, Zeitdauern, oder Risiken sein. Der Vektor \(x\) beinhaltet die Entscheidungsvariablen — Stellgrössen, über deren Wert entschieden werden kann, um die Zielfunktion zu beeinflussen. Die Nebenbedingung \(x \in D\) definiert Beschränkungen, denen die Entscheidungsvariable unterliegt. Wäre \(x\) z.B. eine Materialmenge, dann könnte die Forderung \(x\ge0\) sinnvoll sein.

Relevanz

Werden die drei Komponenten Zielfunktion, Entscheidungsvariablen, und Nebenbedingungen sorgfältig ausgewählt und repräsentieren in Kombination ein Echtweltproblem, dann ergibt die Lösung des Optimierungsproblemes die bestmöglichen Handlungsanweisungen. Deshalb ist Optimierung ein sehr mächtiges Werkzeug, sobald Entscheidungen zu treffen sind, die über weitreichende und unübersichtliche Konsequenzen verfügen. Dabei mag die konkrete Anwendung darin bestehen, Produktparameter zu wählen, Ablaufpläne zu designen, unbekannte Grössen zu schätzen oder Steuerungssignale festzulegen.

Gerade bei komplexen Echtweltproblemen führt dies oft auf mathematische Modelle mit Tausenden von Entscheidungsvariablen und Nebenbedingungen. Das Lösen solcher Modelle ist erst durch das explosionsartige Anwachsen der Rechenleistung moderner Computer und die Entwicklung dedizierter Optimierungssoftware möglich geworden. Mittlerweile wurde eine einheitliche Theorie zur Untersuchung von Optimierungsproblemen entwickelt. Diese hat zu einem Satz von methoden geführt, die bereits oft gewinnbringend in der Praxis angewendet wurden.

Theorie

Optimierungsprobleme treten in allen Formen und Farben auf und können alle Komplexitätskriterien von einfach bis unmöglich abdecken. Zielfunktionen von Optimierungsproblemen können hinsichtlich ihrer mathematischen Eigenschaften untersucht und klassifiziert werden. Sind sie z.B. konvex, dann können Garantien ausgesprochen werden über die eindeutige Lösbarkeit des Problemes.

Oft ist es auch möglich, untere Schranken für die Minima zu finden und so die Optimalität einer vorgeschlagenen Lösung zu beweisen. Dies Zusammenhänge werden von numerischen Methoden verwendet, die iterativ Gleichungssysteme aufstellen und lösen, bis keine Verbesserungen mehr möglich sind.

Methoden

Je nach Eigenschaften des Optimierungsproblemes existieren eventuell massgeschneiderte Methoden zu dessen Lösung. Dabei unterscheidet man vor allem hinsichtlich des Grades der im Optimierungsproblem vorkommenden Nichtlinearitäten sowie der Rolle des Zufalles. Optimierungsprobleme mit linearer Zielfunktion und linearen Nebenbedingungen sind bekannt als Lineare Programme.

Sie können zuverlässig gelöst werden, selbst wenn die Anzahl der Entscheidungsvariablen in die Hunderttausende geht. Nichtlineare Komponenten eines Problemes müssen bestimmte Formen annehmen, um die Lösbarkeit nicht zu gefährden. Ähnliches gilt, sobald zufällige Effekte berücksichtigt werden sollen. Entweder werden die wahrscheinlichkeitstheoretischen Anforderungen in (nichtlineare) Bedingungen umgewandelt oder es muss auf stochastische Simulationen zurückgegriffen werden. Die Entwicklung von hochspezialisierten und leistungsfähigen Algorithmen ist in jedem Fall schwierig. Glücklicherweise gibt es mittlerweile frei verfügbare und quelloffene Software.

Anwendungen

Die praktischen Anwendungen sind vielfältig und schwer überblickbar. das treffen optimaler Entscheidungen als abstrakte Zielvorstellung ist so generell, dass so gut wie jedes Echtweltproblem in Form von Optimierungsproblemen formuliert werden kann. Das heisst natürlich noch lange nicht, dass die auch lösbar sind.

Die grössten Erfolge hat die Optimierung erzielt z.B. bei der Suche nach optimalen Ablaufplänen, Verkehrsrouten, Ressourcenverteilungen, Aktienportfolios, Modellparametersätzen, Wahrscheinlichkeitsverteilungen, Schätzern, Systemsteuerungen und maximal stabilen Spielstrategien. Wir teilen diese heterogene Menge von Anwendungen auf in die Disziplinen optimal design, optimal estimation, und optimal control.

Einordnung

Die Übergänge und Schnittmengen zum Machine Learning sind vielfältig. Da typischerweise jedes Machine Learning Problem als Optimierung von Erfolgswahrscheinlichkeiten geschrieben werden kann, ist die Optimierung ein unveräusserlicher Teilaspekt des datengetriebenen Lernens. mathematische Optimierung ist vielseitig, praxisorientiert, und leistungsfähig. Es ist keine Übertreibung, sie als eine der vielversprechendsten Disziplinen der modernen angewandten Mathematik zu bezeichnen.