Schätzung Korrelationsstrukturen

Optimal estimation: Schätzung von Korrelationsstrukturen

Definition

Korrelationsstrukturen beschreiben die Zusammenhänge zwischen Funktionswerten $f(z_1), … , f(z_n)$ ohne eine explizite Funktionale Form von $f$ vorzuschreiben. Am geläufigsten sind die sogennanten Kovarianzmatrizen $C$. Sie codieren vollständig die Korrelationen aller Funktionswerte untereinander.

Jeder Eintrag von $C$ gibt die Kovarianz zweier Zufallsvariablen $f_i, f_j$ an.

$$ C= \begin{bmatrix} c_{11} & \cdots & c_{1n} \\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn}\end{bmatrix} ~~~~~~ c_{ij}=E[f_if_j]-E[f_i]E[f_j]$$

Dabei ist $E[f_i]$ der Erwartungswert der Zufallsvariable $f_i$. Aus der Gleichung folgt unmittelbar, dass $C$ eine symmetrische Matrix ist mit einer Dimension von $n \times n$, wobei $n$ die Anzahl aller Zufallsvariablen ist.

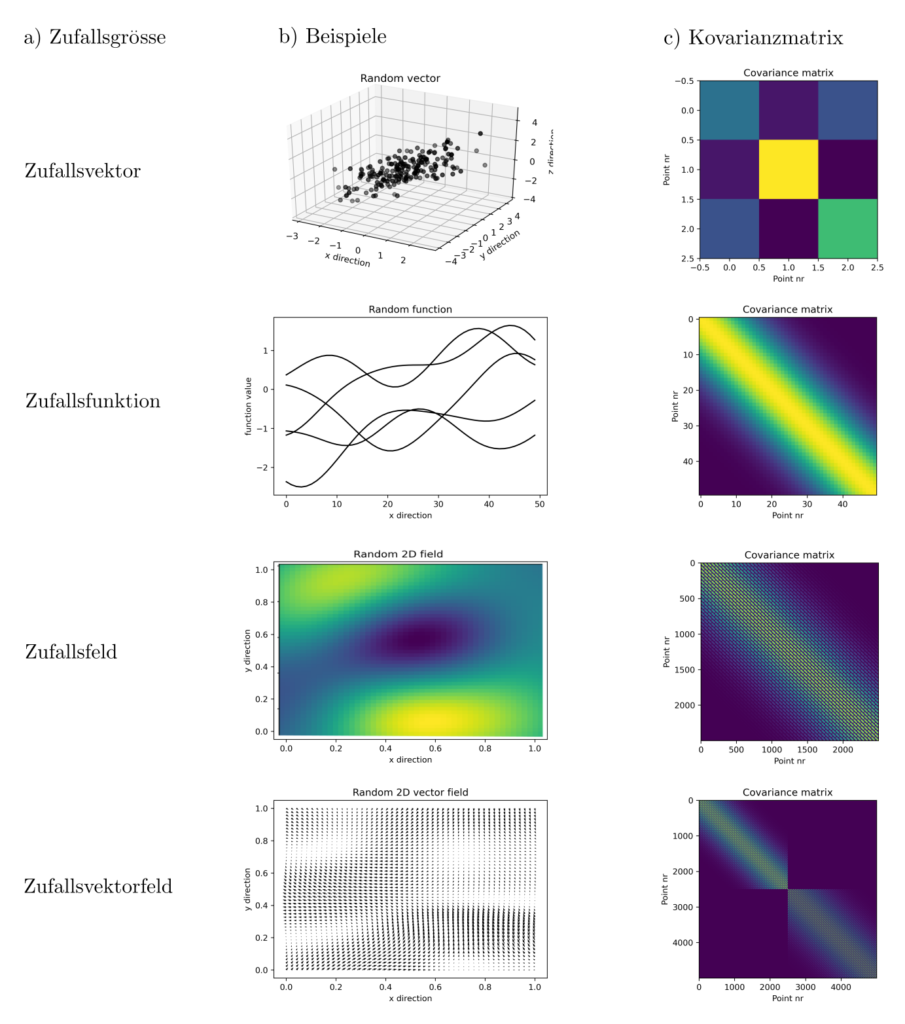
Problem

Sind die Kovarianzmatrizen komplett bekannt, dann sind sie ein wichtiger Bestandteil der Gleichungen für optimal estimation. Oft jedoch ist dies nicht der Fall und es müssen Funktionen $K(z_1,z_2) = E[f_{z_1}f_{z_2}]- E[f_{z_1}]E[f_{z_2}]$ aus punktuell verfügbare Daten $f_1, … ‚f_n$ geschätzt werden. Diese Kovarianzfunktionen $K(z_1,z_2):Z\times Z\rightarrow \mathbb{R}$ werden dann verwendet, um die Kovarianzmatrizen aller für das optimal estimation benötigten Grössen zu generieren.

Die Ableitung der Kovarianzfunktion $K$ aus Daten $f_1, …, f_n$ stellt jedoch eine Herausforderung dar. Da Kovarianzmatrizen zwingend positiv semidefinit sein müssen, muss für $K$ gelten

$$ C\succeq 0 ~~~~~~ C_{ij}=K(z_i,z_j) $$

unabhängig von der konkreten Folge von Auswertepunkten $\{z_i\}_{i=1}^n \subset Z$ [1, p. 11]. Solche $K(\cdot,\cdot)$ heissen positive definite Kerne. $K(\cdot,\cdot)$ aus Daten abzuleiten, erfordert das Lösen eines statistischen Inferenzproblemes unter Nebenbedingungen betreffen das Spektrum von aus $aus K(\cdot,\cdot)$ konstruierbaren Matrizen. Das ist kein einfaches Problem.

Relevanz

Das es trotzdem ein wichtiges Problem ist und eine essentielle Voraussetzung für wirklich zuverlässiges optimal estimation zeigt sich z.B. in den Gleichungen für die Lösung des Interpolationsproblemes. Der optimale Schätzer $f(\cdot)$ auf Basis der Beobachtungen $l=[f(z_1), …, f(z_n)]^T$ ist

$$ \begin{align} f(z) ~~~&= \operatorname{argmin} \|f\|_{\mathcal{H}_K}^2 \\ & ~~~~~\text{s.t.} f(z_j)=l_j ~~~~ j=1, …, n \\ &= \begin{bmatrix} K(z,z_1) & \cdots & K(z,z_n)\end{bmatrix} \begin{bmatrix} K(z_1,z_1) & \cdots & K(z_1,z_n) \\ \vdots & \ddots & \vdots \\ K(z_n,z_1) & \cdots & K(z_n,z_n)\end{bmatrix}^{-1} \begin{bmatrix} l_1 \\ \vdots \\ l_n\end{bmatrix}\\ &= \sum_{j=1}^n \alpha_jK(z,z_j)\end{align}$$

und hängt somit nur ab von den Daten und der Kovarianzfunktion. Für stochastische Prozesse ist das Wissen um die Kovarianzfunktion oft gleichbedeutend mit dem Wissen um die gesamte Wahrscheinlichkeitsverteilung und somit der zentrale Bestandteil der Schätzgleichungen. Folglich ist der Einfluss der Kovarianzfunktion auf den optimalen Schätzer gross.

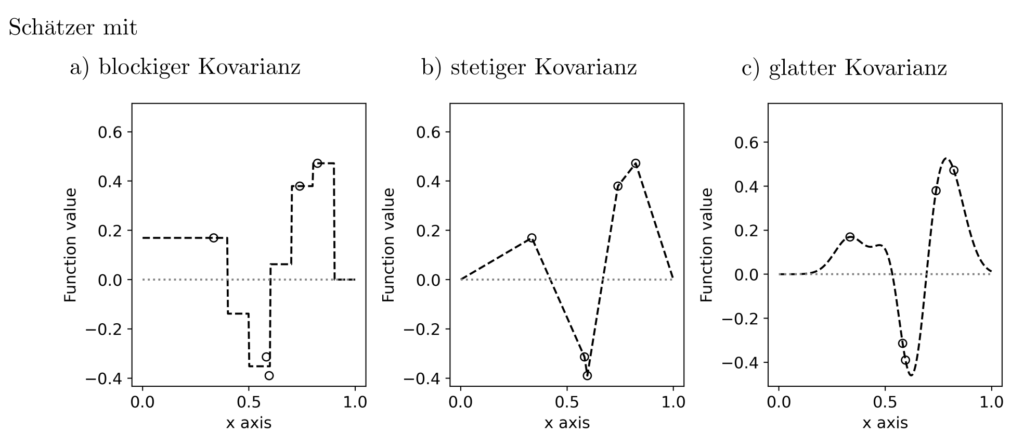
Funktionales Modell Kovarianzfunktionen

Ähnlich der Representation positiv semidefiniter Matrizen $C$ als Produkt $B^TB$ von Matrizen $B$ kann eine Kovarianzfunktion immer geschrieben werden als $ \int_Z B(z_1,z)B(z,z_2)dz$. Unter einigen Annahmen [2, pp. 158–163] impliziert dies eine Zerlegbarkeit von $K(z_1,z_2)$ in

$$ K(z_1,z_2)=\sum_{i=1}^{\infty}\sum_{j=1}^{\infty} \gamma_{ij}\varphi_i(z_1)\varphi_j(z_2) $$

wobei $\varphi_i(z), i=1, … $ eine orthonormale basis von Funktionen auf $Z$ bilden und $\gamma \succeq 0$ eine positiv semidefinite Matrix ist, die ungefähr einer Wishart Verteilung folgt. Dieses Modell ist sehr flexibel und kann eine Vielzahl von Korrelationsstrukturen erzeugen.

Inferenzgleichungen

Nimmt man an, $K(z_1,z_2)$ sei ein Quadrat $B^TB = \int_Z B(z_1,z)B(z,z_2)dz$ normalverteilert zufälliger Funktionen $B$, dann ist $\gamma$ ungefähr Wishart verteilt. Mit $p(l|\gamma)$ der bedingten Wahrscheinlichkeit von Beobachtungen $l$ gegeben die Kovarianzfunktion in Abhängigkeit von $\gamma$ sowie $p(\gamma)$ der Wahrscheinlichkeit von $\gamma$ gilt nach Bayes-theorem

$$p(\gamma|l) = c p(l|\gamma)p(\gamma) ~~~~~~ c \text{ eine Konstante}.$$

Dabei ist $p(\gamma|l)$ die bedingte Wahrscheinlichkeit von $\gamma$, wenn $l$ beobachtet wurde. Maximierung der Wahrscheinlichkeit ist gleichbedeutend mit Minimierung von $-\log p(\gamma|l)=-\log p(l|\gamma)-\log p(\gamma)$.

Das Optimierungsproblem lautet

$$ \begin{align} \min_{\gamma} ~~~& \log \det C_{\gamma} + \operatorname{tr} (SC_{\gamma}^+)+ r\left[ — \log \det \gamma + \operatorname{tr}(\Lambda^+\gamma)\right] \\ \text{s.t.}
~~~& A \gamma =b \\ ~~~& \gamma \succeq 0 \end{align}$$

wobei $S$ die empirische Kovarianzmatrix der Daten $l$, $C_{\gamma}$ die mit Hilfe von $\gamma$ rekonstruierte Kovarianzmatrix, $C_{\gamma}^+$ deren Pseudeinverse und $\Lambda$ eine Matrix ist, die a‑priori Annahmen über $\gamma$ codiert. Die Regularisierungskonstante $r$ gewichtet Vorwissen und Daten gegeneinander und $A \gamma = b$ sind lineare Bedingungen für $\gamma$. Sie repräsentieren definitives Wissen über der Korrelationsstruktur zugrundeliegende Zusammenhänge. Mit den Informationen über erste und zweite Ableitungen der Zielfunktion ergibt sich das numerische Schema [2, p. 194]

$$ \begin{align} \gamma &= \gamma +\Delta \gamma ‑A^T(A\gamma A^T)^+A\Delta \gamma \\ \Delta \gamma & = \frac{1}{1+r} \left[ (r‑1)\gamma +S_{\psi} — r\gamma \Lambda^+\gamma\right] \end{align}$$

wobei $S_{\psi}$ eine transformierte Variante der empirischen Kovarianzmatrix ist. Werden die iterationen über $\gamma$ numerisch stabilisiert und bis zur Konvergenz ausgeführt, dann ist das Resultat eine mit Hilfe von $\gamma$ konstruierte Kovarianzfunktion $ K(z_1,z_2)$. Sie sagt für alle möglichen Positionen $z_1, z_2$ Korrelationen vorher, die maximal konsistent sind mit den punktuellen Beobachtungen $l$ und den Vorannahmen.

Resultate

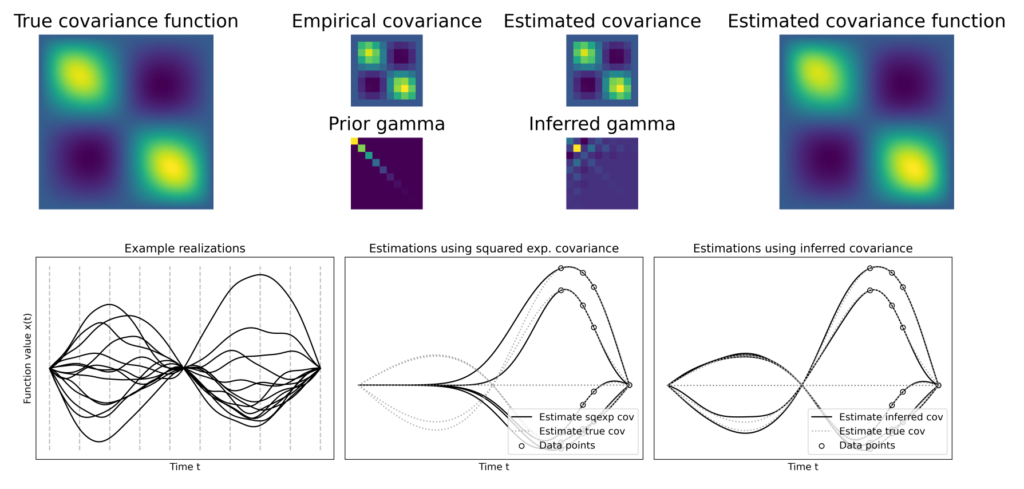
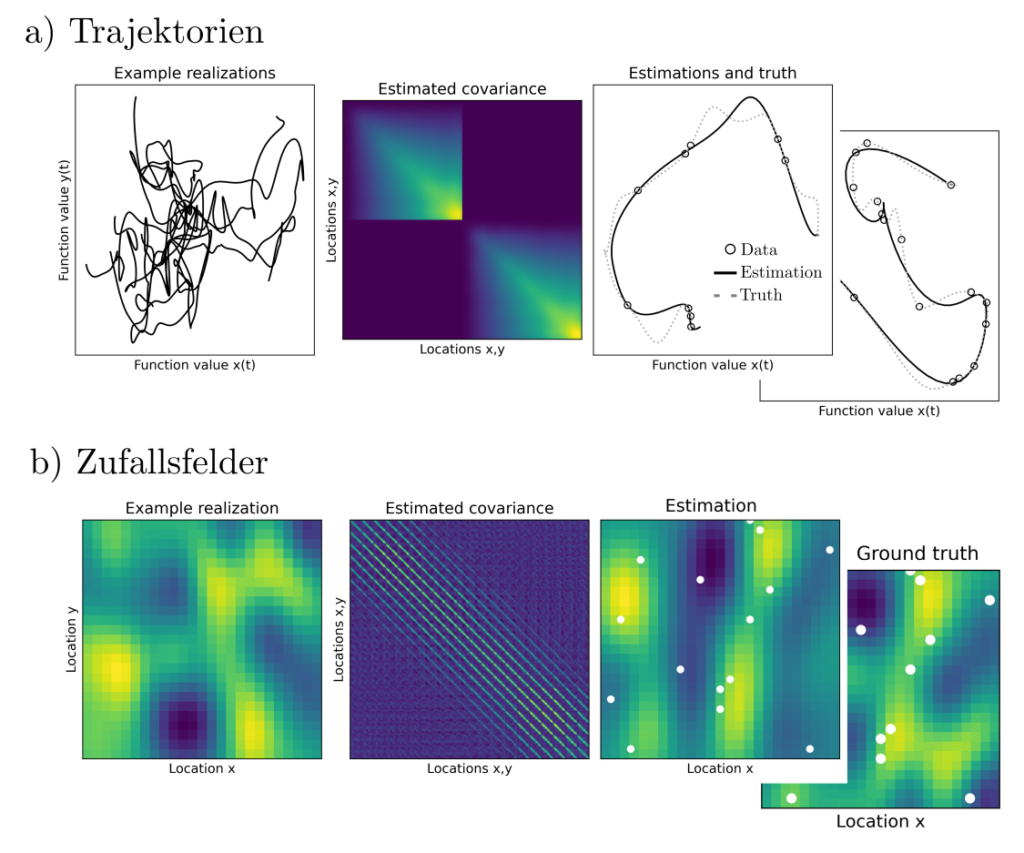
Die optimale Schätzung von Korrelationsstrukturen mit der obigen methode ist flexibler als klassische Vorgehensweise basierend auf der subjektiven Wahl parametrischer Familien von Kovarianzfunktionen. Eine Vielzahl von Echtweltprozessen kann hinsichtlich ihrer Korrelationsstruktur nicht durch einfache Funktionen dargestellt werden.

Die stochastische Modellierung solcher Prozesse profitiert von der Flexibilität der obigen Methode. Dies wird besonders klar, wenn die aus verschiedenen methoden gewonnenen Kovarianzfunktionen im rahmen der optimalen Schätzung von Funktionen verwendet werden.

Abbildung 4 : Die zugrundeliegende wahre Kovarianzfunktion ist typischerweise unbekannt. Nur einzelne Messungen sind zugänglich sowie eine Vermutung über z.B. Glattheitseigenschaften der Kovarianzfunktion. Werden Daten und Vorwissen kombiniert, entsteht eine Kovarianzfunktion, die der wahren sehr ähnelt. Man bemerke, dass diese Kovarianzfunktion zu deutlich besseren Interpolationen führt als eine generische Kovarianzfunktion.

Erweiterungen

Das Schätzverfahren kann ausgedehnt werden auf Situationen, in denen sowohl Mittelwerte als auch Kovarianzen unbekannt sind und Beobachtungen $l$ in $m$ verschiedenen Gruppen $(l^1_1, …, l^1_{n_1}, … l^m_1, …, l^m_{n_m}$ mit verschiedenen Aufnahmemethodiken anfallen. Das zugehörige Optimierungsproblem

$$ \begin{align} \min_{\beta, \gamma} ~~~& \sum_{i=1}^m \log \det \eta_i +
\operatorname{tr} (S_{\phi}^i\eta_i^+)+ r\left[ — \log \det \gamma +
\operatorname{tr}(\Lambda^+\gamma)\right] \\ \text{s.t.}
~~~& A \gamma =b \\ &F_i\gamma -\eta_i= 0 ~~~~ i=1, …, m \\ ~~~& \gamma \succeq 0 \\ & \eta_i \succeq 0 ~~~~ i=1, …, m \end{align}$$

wobei $\eta_i i=1, …, m$ Kovarianzmatrizen sind, die via $F_i\gamma-\eta_i=0$ an $\gamma$ gekoppelt werden und $S_{\phi}^i$ transformierte empirische Kovarianzmatrizen. Die Optimierung kann mittels projiziertem Newtonverfahren durchgeführt werden, siehe z.B. hier (Github Link). Die Erweiterung auf multiple Dimensionen ist trivial.

Praktisches

Die Schätzung von Korrelationsstrukturen ist sehr wichtig für die Generierung aussagekräftiger stochastischer Modelle. Sie ist daher ein häufig angetroffenes Diskussionsthema in der räumlichen Statistik, der Analyse physikalsicher Prozesse, der Verwendung von Regressionsmodellen und im maschinellen Lernen.

Sind genug Daten vorhanden, so kann ein von hand auf Basis von Vermutungen erstelltes stochastisches Modell verfeinert werden. das hat positive Auswirkungen auf die Qualität der mit Hilfe des Modells abgeleiteten Aussagen.

Code & Quellen

eispielcode: OE_KI.py , OE_KI_support_funs.py , OE_KI_covariance_impact_1.py, OE_KI_covariance_impact_2.py , OE_KI_interpolate_brownian_bridge.py , OE_KI_interpolate_field.py , OE_KI_interpolate_function.py , OE_KI_interpolate_trajectgory.py in unserem Tutorialfolder.

[1] Berlinet, A., & Thomas-Agnan, C. (2011). Reproducing Kernel Hilbert Spaces in Probability and Statistics: . Berlin Heidelberg: Springer Science & Business Media.

[2] Butt, J. A. (2019). An RKHS approach to modelling and inference for spatiotemporal geodetic data with applications to terrestrial radar interferometry. Dissertation ETH Zürich, Zürich.