Semidefinite programming - Atlas optimization

Methoden: Semidefinite programming

Definition

nter dem Begriff semidefinite programming (SDP) werden Optimierungsprobleme mit linearer Zielfunktion zusammengefasst, deren Nebenbedingungen aus linearen Gleichungen und spektralen Ungleichungen bestehen.

Die letzteren quantifizieren Anforderungen an das Spektrum (die Eigenwerte) von aus den Optimierungsvariablen konstruierten Matrizen. Zentral sind demnach Optimierungsprobleme

$$ \begin{align} \min_x ~~~& \langle c, x\rangle \\ \text{s.t.}
~~~&Ax =b \\ ~~~& \sum_{k=1}^n x_k G_k \succeq 0 \end{align}$$

in der Optimierungsvariablen $x$ [1, p. 168]. Dabei sind $x, c, b$ Vektoren, $A, G_1, …, G_n, H$ sind Matrizen und für eine Matrix $ F$ besagt $F\succeq 0$, dass das Spektrum von $F$ positiv sei. $F \succeq 0$ ist eine globale Aussage über bestimmte Kombinationen aller Elemente von $F$ gemeinsam und lässt sich nicht vereinfachen zu elementweisen Ungleichungen. Das obige Problem in detaillierter Schreibweise lautet wie folgt.

Finde die Variablen $x_1, …, x_n$ sodass $\langle c,x\rangle = c_1x_1 +, … , +c_nx_n$ minimal wird
Dabei soll gelten:
1. $a_{k1} x_1 + , …, + a_{kn}x_n =b_k ~~~~k=1, …, m_1$
2. $x_1 G_1 + , …, + x_n G_n \succeq H$

Wie auch beim LP besteht das Problem aus der Minimierung einer Summe $\langle c,x\rangle$, $m_1$ Gleichungen, und Ungleichungen. Im Gegensatz zum LP betreffen die Ungleichungen das Spektrum einer Matrix $x_1G_1 + , …, + x_nG_n‑H$, wodurch sie ungleich flexibler aber auch schwieriger zu interpretieren sind. SDP ist sehr generell und inkludiert LP, QP, QCQP, und SOCP [2, p. 3].

Beispiel

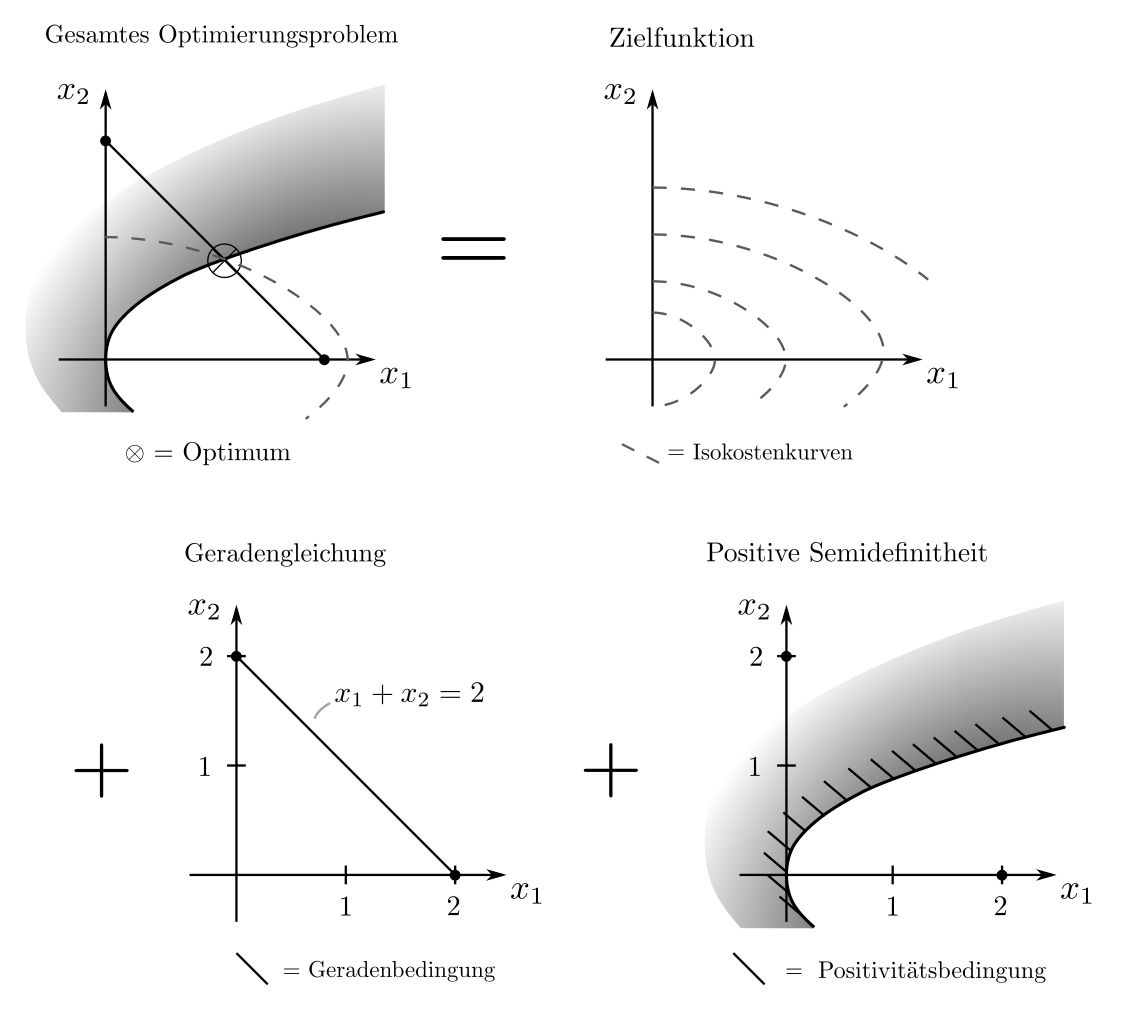
Jedes Beispiel für LP, QP, QCQP, und SOCP ist auch ein Beispiel für SDP. SDP sind besonders geeignet für Optimierungsaufgaben betreffend Eigenwerte von Matrizen und damit z.B. für die Minimierung von Unsicherheitsmassen. Es sei die Matrix

$$ \begin{align} F=\begin{bmatrix} x_1 & x_2 \\ x_2 &1 \end{bmatrix} \succeq 0 ~~~~~ x_1+x_2=2 \end{align}$$

die Kovarianzmatrix, ein Mass für die Unsicherheiten und Korrelationen in Experimenten. Dabei sind $x_1$ und $x_2$ Entscheidungsvariablen betreffend der Wahl von Experimenten. Sie sollen so gewählt werden, dass der grösste Eigenwert von $F$ — als Indikator für die maximale Unsicherheit — minimal wird. Mittels einiger Transformationen [1, p. 387] kann das Problem als das SDP

$$ \begin{align} \min_{x_1, …, x_n, t} ~~~& t \\ \text{s.t.}
~~~&x_1+x_2 =2 \\ ~~~& t \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} — \begin{bmatrix} x_1 & x_2 \\ x_2 & 1 \end{bmatrix} \succeq 0 ~~~~\begin{bmatrix} x_1 & x_2 \\ x_2 & 1 \end{bmatrix} \succeq 0 \end{align}$$

geschrieben werden. Mittels CVXPY [3] und des integrierten SCS Algorithmus’ [4] ergibt sich die nichttriviale Lösung $x_1=1.6, x_2=0.4$.

Anwendungen

Die Anwendungsmöglichkeiten von SDP sind enorm vielseitig und beinhalten alle Probleme, bei denen das Spektrum von Matrizen relevant ist. Dazu zählen viele wahrscheinlichkeitstheoretische und physikalische Probleme; vor allem aus optimaler Steuerung, Systemstabilisierung, Regelungstechnik, Portfoliooptimierung, Experimentendesign, statistischen Ungleichungen, Robuster Approximation und Entscheidungsfindung, Baustatischem Design, Optimierung unter probabilistischen Nebenbedingungen sowie der Suche nach Approximationslösungen für schwere kombinatorische Probleme wie etwa Max Cut oder die Optimierung von quadratischen Formen auf Graphen. Details sind hier zu finden.

Die Optimierungsvariablen $x_1, …, x_n$ sind oft als Parameter von Kovarianz- oder Energiematrizen zu interpretieren. Durch diverse Tricks zur Formulierung von SDPs sind sie oft äusserst schwierig zu verstehen. Als Beispiel mag die Einbettung von SOCPs dienen. Diese Optimierungsprobleme der Form

$$ \begin{align} \min_x ~~~& \langle c, x\rangle \\ \text{s.t.}
~~~&Ax =b \\ ~~~& \|G_k x +h_k\|_2 \le \langle f_k,x\rangle + d_k ~~~ k=1, …, m_2 \end{align}$$

lassen sich mit Hilfe des Schur-Komplementes reformulieren als das SDP

$$ \begin{align} \min_x ~~~& \langle c, x\rangle \\ \text{s.t.}
~~~&Ax =b \\ ~~~& \begin{bmatrix} r_kI & q_k \\ q_k^T & r_k \end{bmatrix} \succeq 0 ~~~k=1, …, m_2 \end{align}$$

Dabei ist $I$ die EInheitsmatrix, $r_k=\langle f_k,x\rangle +d_k, q_k=G_kx+h_k$ und die Äquivalenz ergibt sich aus $[A ~~b ; b^T~~ c] \succeq 0 \Leftrightarrow A\succeq 0 \wedge c- b^T Ab\succeq 0$.

Lösungsverfahren

Semidefinite Programme sind seit den frühen 2000ern mit offen zugänglicher Software zu lösen. Theoretische Algorithmen existieren seit den 1980ern [5]. Wie das illustrierte Beispiel zeigt, bedinden sich die Optima nicht zwangsläufig am rand der zulässigen menge, was Verfahren nach Art der Simplex-Methode ausschliesst.

Stattdessen kommen interior-point methods zum Einsatz, die Bedingungen vom Typ $X\succeq0$ ersetzen durch die Barrierefunktionen $-\mu \log \det x$, die am Rand der zulässigen Menge explosionsartig anwächst. Wird $\mu$ sukzessive verkleinert, so strebt das Minimum von $\langle c,x\rangle — \mu \log \det x$ gegen $ \min_x \langle c,x\rangle$ mit $x\succeq 0$ [6, p. 286]. Die zulässigen Mengen sind nichtlinear und der Pfad durch die menge wird von den lokalen Gradienten gestuert, siehe Abbildung.

Praktisches

SDP mit einigen zehntausend Variablen können heutzutage zuverlässig gelöst werden. Die entsprechenden Algorithmen sind entwickelt und in Form von open source Software implementiert worden. SCS [4], SeDuMi [8] und SDPT3 [9] sind öffentlich verfügbar — die Software ist jedoch numerisch instabiler als vergleichbare Gleichungslöser für LP oder QP. Da die Nebenbedingungen beim SDP als unendlich viele lineare Ungleicungen aufgefasst werden können, ist SDP eine sehr umfangreiche Problemklasse. Die Modellierung als spektral beschränktes Optimierungsproblem ist jedoch eine Herausforderung.

Code & Quellen

Beispielcode: Methods_sdp.py in unserem Tutorialfolder

[1] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.

[2] De Klerk, E. (2006). Aspects of Semidefinite Programming: Interior Point Algorithms and Selected Applications. Berlin Heidelberg: Springer Science & Business Media.

[3] Diamond S., & Boyd S., (2016). CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research, 17(83), 1–5.

[4] O’donoghue, B., Chu, E., Parikh, N., & Boyd, S. (2016). Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. Journal of Optimization Theory and Applications, 169(3), 1042–1068.

[5] Karmarkar, N. (1984). A new polynomial-time algorithm for linear programming. Combinatorica, 4, 373–395.

[6] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.

[7] Vinzant, C. (2014). What is … a spectrahedron? Notices of the American Mathematical Society, 61, 492–494.

[8] Sturm, J. F. (1999). Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optimization Methods and Software, 11(1–4), 625–653.

[9] Tütüncü, R. H., Toh, K. C., & Todd, M. J. (2003). Solving semidefinite-quadratic-linear programs using SDPT3, Mathematical Programming, 95, 189–217.