Optimal design: Experimentendesign
Problemstellung

Die Frage nach der optimalen Ausgestaltung eines Experimentes oder einer Messanordnung tritt überall dort auf, wo die Erhebung von Messungen kostenintensiv und mit Unsicherheiten behaftet ist.
Die betrifft jegliche Anwendungen, bei denen die Datenauswertung mit statistischen methoden vorzunehmen ist wie z.B. bei dem Entwurf von pharmazeutischen Versuchsreihen [1, p. 511], schulischen Examen [2], oder Messnetzen in der Geodäsie [3]. Beim Experimentendesign ist herauszufinden, wie oft welche Messungen auszuführen sind, um den Informationsgehalt der Daten zu maximieren.
Beispiel: Messverteilung
Es soll eine Gerade durch an zwei Positionen gemessene Datenpunkte gelegt werden. Dies alleine wäre eine triviale Aufgabe aus dem bereich der Parameterschätzung. Wir beschäftigen uns jetzt jedoch mit der Fragestellung, wie ein Messbudget von z.B. \(N=10\) verrauschten Messungen auf diese Positionen so aufgeteilt werden kann, dass die Gesamtunsicherheit der geschätzten Gerade minimiert wird. Dies ist genau ein Problem des Experimentendesigns.
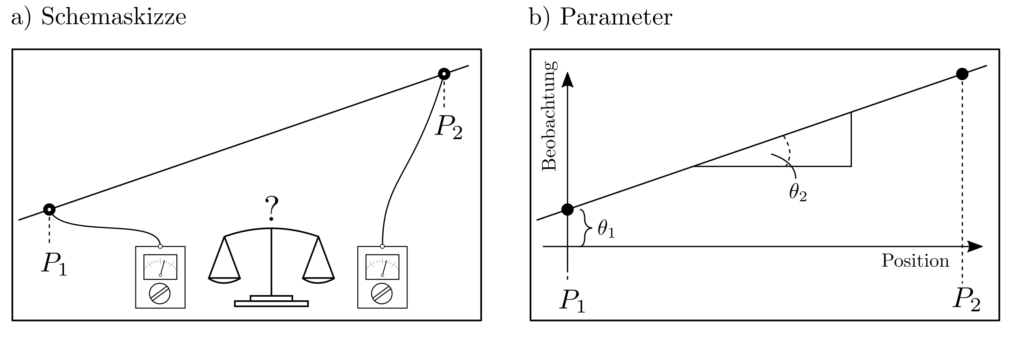
Der Zusammenhang zwischen Messungen \(l_1\), \(l_2\) und Positionen \(p_1, p_2\) ist aufgrund der Geradengleichung gegeben als
$$ \underbrace{\begin{bmatrix} l_1 \\ l_2 \end{bmatrix}}_{l}\approx \underbrace{\begin{bmatrix} 1 & p_1 \\ 1 & p_2 \end{bmatrix}}_{A} \underbrace{\begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}}_{\theta} ~~~~~\begin{matrix} \theta_1 : \text{ Abszisse} \\ \theta_2 : \text{ Steigung} \end{matrix}.$$
Es können \(n_1\) Messungen an \(p_1\) durchgeführt werden und \(n_2\) Messungen an \(p_2\) wobei \(n_1+n_2=N=10\) gelten soll.
Beispiel: Optimierungsformulierung
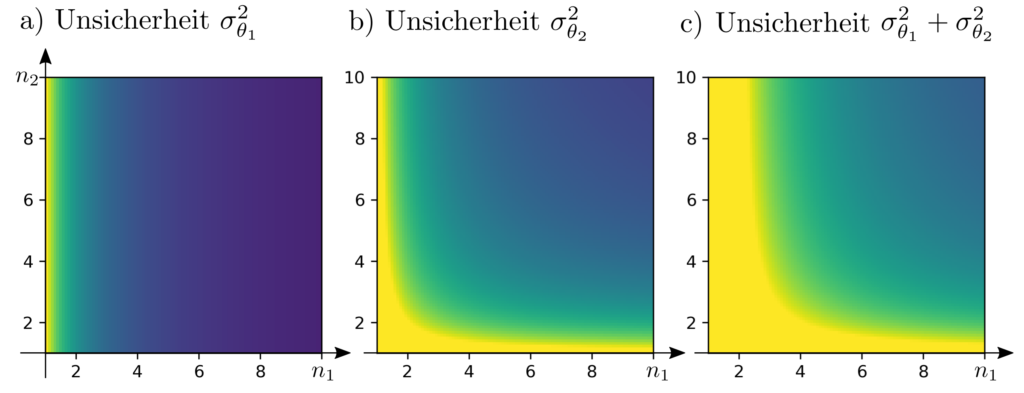
Diese Messverteilung ist so zu wählen, dass die Gesamtunsicherheit \(\sigma_{\theta_1}^2 + \sigma_{\theta_2}^2\) der Parameter minimiert wird. Dabei ist \(\sigma_{\theta}^2\) die varianz des Parameters \(\theta\). Das Optimierungsproblem lautet
$$\begin{align} \min_{n_1,n_2} ~~~ & \sigma_{\theta_1}^2(n_1,n_2) + \sigma_{\theta_2}^2 (n_1, n_2) \\ \text{s.t.} ~~~ & n_1+n_2=10 \end{align}$$
Der Einfachheit halber nehmen wir an, die Messungen seien gleichgenau mit Varianz \(\sigma_0^2\) und wählen die konkreten Messpositionen \(p_1=0\) und \(p_2=1\). Gemäss den üblichen Rechenregeln für Unsicherheiten, verrignert eine \(n-\) fache Messung die Varianz auf das \(1/n-\) fache der Einzelmessung [4, p. 17]. Dann gilt für die Kovarianzmatrizen \(\Sigma_l, \Sigma_{\theta}\) der Beobachtungen und der Parameter
$$\begin{align} \Sigma_l & = \sigma_0^2 \begin{bmatrix} \frac{1}{n_1} & 0 \\ 0 & \frac{1}{n_2} \end{bmatrix} \\ \Sigma_{\theta} & =A^{-1} \Sigma_l A^{-1 T} \\ & = \sigma_0^2 \begin{bmatrix} 1 & 0 \\ ‑1 &1 \end{bmatrix} \begin{bmatrix} \frac{1}{n_1} & 0 \\ 0 & \frac{1}{n_2} \end{bmatrix} \begin{bmatrix} 1 & ‑1 \\ 0 & 1 \end{bmatrix} \\ & = \sigma_0^2 \begin{bmatrix} \frac{1}{n_1} & — \frac{1}{n_1} \\ -\frac{1}{n_1} & \frac{1}{n_1}+\frac{1}{n_2} \end{bmatrix} \end{align} $$
Minimierung von \(\sigma_{\theta_1}^2 + \sigma_{\theta_2}^2\) ist gelichbedeutend mit Minimierung von \(\operatorname{tr} \Sigma_{\theta} \) und das optimale Experimentendesign zeichnet sich demnach aus durch
$$\begin{align} \min_{n_1,n_2} ~~~& \frac{2}{n_1}+\frac{1}{n_2} \\ \text{s.t.} ~~~ & n_1+n_2=10 \end{align}$$
Beispiel: Lösung
Überraschenderweise ist die Messung an der Stelle \(p_1\) doppelt so wichtig für die gesamtunsicherheit wie die Messung an der Stelle \(p_2\). Die rührt daher, dass die Messung \(l_2\) irrelevant ist für den Parameter \(\theta_1\) — ein Zusammenhang der bei einer intuitiven gleichverteilung der Messungen nicht berücksichtigt worden wäre.
Das beschränkte Optimierungsproblem lässt sich lösen mit Hilfe der Lagrangefunktion \(\mathcal{L}\) und der dazugehörigen KKT Gleichungen.
$$ \begin{align} \mathcal{L}(n_1,n_2,\nu)&= \frac{2}{n_1}+\frac{1}{n_2}+\nu(n_1+n_2-10) \\ \partial_{n_1} \mathcal{L} & = -\frac{2}{n_1^2}+\nu\stackrel{!}{=}0 \\\partial_{n_2} \mathcal{L} &=-\frac{1}{n_2^2}+\nu \stackrel{!}{=}0 \\ \partial_{\nu} \mathcal{L} & = n_1+n_2-1- \stackrel{!}{=} 0 \end{align}$$
Die optimale Lösung ist \(n_1^*=(1+\sqrt{2})^{-1}(\sqrt{2} +10)\approx 5.9 \) und \(n_2^*=(1+\sqrt{2})^{-1}10 \approx 4.1\). Die minimale Unsicherheit der Parameter beträgt \(0.583*\sigma_0^2\) wobei \(\sigma_0^2\) die Varianz einer Einzelmessung ist.
Generalisierung
Diverse Erweiterungen des Problemes sind möglich. Zu verschiedenen Messungen können verschiedene Kosten assoziiert werden und Messungen können miteinander gekoppelt werden. Es ist auch möglich, Messungen zu Gruppen zusammenzufassen und Entscheidungen über das Experimentendesign nur auf Ebene dieser Gruppen zuzulassen. Üblicherweise wird das Optimierungsproblem zur Ermittlung bester Experimentendesigns mit Hilfe der Fisher-Informationsmatrix \(\mathcal{M}\) formuliert zu [1, p. 514]
$$\begin{align} \min_{\xi} ~~~ & \Psi[\mathcal{M}] \\ \text{s.t.} ~~~& \xi \in \Xi \\ & \xi = \begin{bmatrix} p_1 & \cdots & p_n \\ x_1 & \cdots & x_n \end{bmatrix} \end{align} .$$
Dabei ist \(\xi\) das Design des Experimentes, welches die Messpunkte \(p_1, …, p_n\) und die relativen Häufigkeiten \(x_1, …, x_n\) der Messungen festlegen. Es ist auf die menge \(\Xi\) beschränkt und die sich aus dem Design \(\xi\) ergebende Informationsmatrix \(\mathcal{M}\) wird hinsichtlich ihrer tauglichkeit durch die Funktion \(\Psi\) beurteilt. \(\Psi(\mathcal{M}\) steht meist in direktem Bezug zu der Kovarianzmatrix \(\Sigma_{\theta}\) der aus dem Experiment abzuleitenden Parameter und kann etwa die Gesamtunsicherheit \(\operatorname{tr} \Sigma_{\theta}\), die Maximalunsicherheit \(\lambda_{max} (\Sigma_{\theta})\), oder das Unsicherheitsvolumen \(\log \det \Sigma_{\theta}\) sein [1, pp. 511- 532].
Das obige Optimierungsproblem generalisiert die anfänglich manuell gelöste Aufgabenstellung betreffend die optimale Messverteilung zur Parameterbestimmung einer Ausgleichsgerade. In ihr waren \(n=2, p_1\) und \(p_2\) waren fixiert und \(x_1=n_1, x_2=n_2\) waren so zu wählen, dass \(\Psi(\mathcal{M})=\operatorname{tr} \Sigma_{\theta} =\sigma_{\theta_1}^2+\sigma_{\theta_2}^2\) minimal wird. Der Zusammenhang zwischen \(\Sigma_{\theta}\) und \(l \approx A \theta\) war \(\Sigma_{\theta} = A^{-1}\Sigma_l A^{-1 T}\) und somit $$ \Sigma_{\theta} = A^{-1} \begin{bmatrix} \frac{1}{n_1} & 0 \\ 0 & \frac{1}{n_2} \end{bmatrix} A^{-1 T} = A^{-1} \begin{bmatrix} n_1 & 0 \\ 0 & n_2\end{bmatrix}^{-1} A^{-1 T} = \left[ \sum_{k=1}^2 n_k a_k a_k^T\right]^{-1} $$
wobei \(a_1, a_2\) die Zeilen der Matrix \(A\) sind.
Optimierungsformulierung Gesamtunsicherheit
praktisch generalisiert sich die von uns im einfachen 2‑dimensionalen Fall durchgeführte Gesamtunsicherheitsminimierung als semidefinites Programm der folgenden Form [5, p. 387].
$$ \begin{align} \min_x ~~~& \operatorname{tr}\left[\sum_{k=1}^n x_k a_k a_k^T\right]^{-1} \\ \text{s.t.} ~~~& x \ge 0 ~~~ \vec{1}^Tx=1 \end{align}$$
Hierbei ist \(C=[\sum_{k=1}^n x_k a_k a_k^T]^{-1}\) eine Kovarianzmatrix. Die Ausdehnung von \(C\) minimal zu halten über die Forderung \( \min _x \operatorname{tr} C\) impliziert geringstmögliche Unsicherheiten. In der Optimierungsformulierung sind die Einträge \(x_k, k=1, …, n\) des Vektors \(x\) die Entscheidungsvariablen. Ihre Werte geben an, wie gross der Anteil von Versuch Nr. \(k\) ist am gesamten Versuchsbudget. Daher müssen die \(x_k\) auch nicht-negativ sein und sich zu 1 addieren. Die \(a_k, k=1, …, n\) repräsentieren \(n\) verschiedene potentielle Messungen.
Das Problem kann mit Hilfe des Schur-Komplementes in ein semidefinites Programm in Standardform umgewandelt werden. In der Form
$$ \begin{align} \min_{x, u} ~~~& \vec{1}^Tu \\ \text{s.t.} ~~~& x \ge 0 ~~~ \vec{1}^Tx=1 \\ & \begin{bmatrix} \sum_{k=1}^n x_k a_k a_k^T & e_k \\ e_k^T & u_k\end{bmatrix} \succeq 0 ~~~~~~k=1, …, n \end{align}$$
weist es lineare Matrixungleichungen auf und kann z.B. mit Hilfe des Open source solvers SCS [6] gelöst werden.
Anwendung
Das automatische Experimentendesign via Optimierungsalgorithmus wird mit einem Beispiel illustriert. Es gelte wieder
$$ l\approx A \theta $$
wobei \(A\) eine Matrix ist und \(\theta\) mehrere unbekannte Wirkeigenschaften eines Produktes (z.B. einer Chemikalie) sind. Der Bestmögliche Schätzer für \(\theta\) ist \(\hat{\theta}=(A^TA)^{-1}A^Tl\) mit Kovarianzmatrix \(C=(A^TA)^{-1}\). Wähle nun die Einträge von \(A\) so, dass \(C\) klein wird. Dabei stehen die Versuche \(a_1, …, a_{10}\) zur Auswahl, deren Häufigkeit zu wählen ist.
$$ a_1=\begin{bmatrix} 1.62 \\ ‑0.61 \\ ‑0.53 \end{bmatrix} ~~~~ … ~~~~ a_3=\begin{bmatrix} 1.74 \\ ‑0.76 \\ 0.32 \end{bmatrix} ~~~~ … ~~~~ a_8=\begin{bmatrix} 1.14 \\ 0.90 \\ 0.50 \end{bmatrix} ~~~~ … ~~~~ a_{10} =\begin{bmatrix} ‑0.93 \\ ‑0.26 \\ 0.53 \end{bmatrix} $$
Das Finden einer Verteilung \(x\) von Messungen, sodass \(\operatorname{tr} ( \sum_{k=1}^{10} x_k a_ka_k^T)^{-1} \) minimal wird ist eine semidefinites Programm, das sich innerhalb von 0.1 Sekunden auf einem Officecomputer lösen lässt.
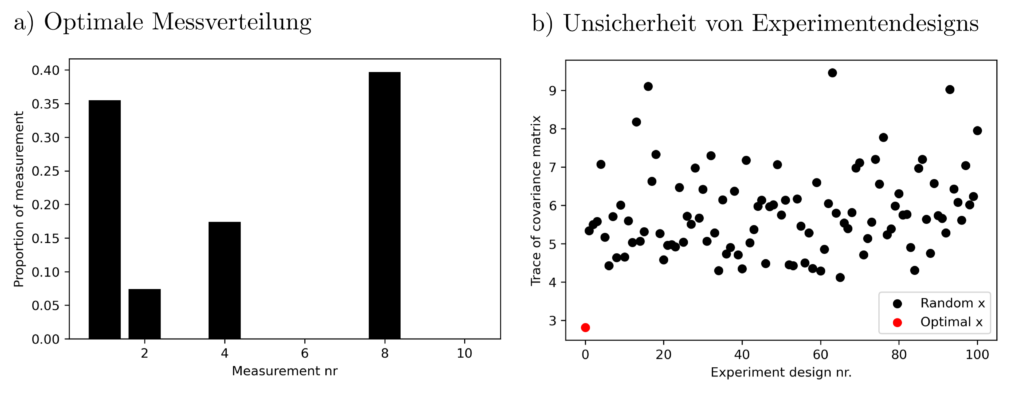
Das Ergebnis lässt einige Schlüsse zu. So ist z.B. Versuch Nr. 3 der Genauigkeit bei der Wirkungsgradschätzung nur wenig zuträglich und Versuch Nr. 2 ist besonders aussagekräftig. Die obige Lösung des Optimierungsproblemes erzielt signifikant bessere (=kleinere) Varianzen als sonstige, zufällig gewählte Experimentenkonfigurationen.
Praktisches
Optimales Experimentendesign ist besonders dann wichtig, wenn die Datenerhebung mit grossem Aufwand und hohen Kosten verbunden ist und die Eigenschaften des zu untersuchenden Objektes unklar sind. Besondere Schwierigkeiten treten dann auf, wenn Korrelationen oder Kausalitäten das stochastische Modell \(l \approx A\theta\) verkomplizieren. Gleiches gilt für nichtlineare Zusammenhänge, die eine Formulierung als wohldefiniertes semidefinites Programm unterbinden.
Sind allerdings gewisse Standardvorraussetzungen gegeben, dann ist optimales Experimentendesign selbst mit hunderten von zu treffenden Messentscheidungen routinemässig möglich und die Interpretation der garantierten Gütekriterien ist relativ einfach.
Code & Quellen
eispielcode: OD_experiment_design_1.py, OD_experiment_design_2 in unserem Tutorialfolder
[1] Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2012). Handbook of Semidefinite Programming: Theory, Algorithms, and Applications. Berlin Heidelberg: Springer Science & Business Media.
[2] Fletcher, R. (1981) A nonlinear Programming Problem in Statistics (Educational Testing). SIAM Journal on Scientific and Statistical Computing, 2(3), 257–267.
[3] Grafarend, Erik W., Sansò, F. (2012). Optimization and Design of Geodetic Networks. Berlin Heidelberg: Springer Science & Business Media.
[4] Ash, Robert B. (2011). Statistical Inference: A Concise Course. New York: Courier Corporation.
[5] Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.
[6] O’donoghue, B., Chu, E., Parikh, N., & Boyd, S. (2016). Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. Journal of Optimization Theory and Applications, 169(3), 1042–1068.
