Methoden: Dynamic programming
Definition
Dynamic programming (DP) behandelt Optimierungsprobleme, in denen die Optimierungsvariablen Abfolgen von Entschiedungen repräsentieren. Die Sequentialität wird zur Herstellung rekursiver Zusammenhänge verwendet.
Diese Rekursivität zerlegt das Gesamtproblem in eine effizient zu lösende Abfolge von aufeinander aufbauenden Subproblemen. Damit ist DP gleichsam ein Lösungsansatz als auch eine Problemklasse. Wir interpretieren DP zwecks Verständlichkeit enger als zwingend nötig als das Optimierungsproblem
$$ \begin{align} \min_{\pi} ~~~& f(\pi) \\f(\pi)
~~~&= \sum_{k=1}^{end} E\left[ r(s_k, s_{k+1}, \pi(s_k))\right] \end{align}$$
in der Optimierungsvariable \(\pi\) [1, p. 23]. Die Besonderheit besteht in der Interpretation von \(f(\pi)\) als erwarteter Belohnung \(E[r]\) in Reaktion auf von Systemzuständen \(s_k\) abhängigen Aktionen \(\pi(s_k)\). Ziel ist das Finden einer Policy \(\pi\), welche Systemzustände auf diejenigen Steuerungsinputs abbildet, die das System im Mittel optimal steuern. Dabei wird die Güte einer Lösung durch die kumulative Menge gesammelter Belohnung \(r\) gemessen.
Beispiel
Man stelle sich etwa eine laufende Bestandsplanung vor, für welche auf Basis der aktuellen Bestände und der im Laufe der Zeit bekanntwerdenden Absatzmöglichkeiten kostenminimierende Entscheidungen getroffen werden müssen. Bestandsdefizite sorgen für Gewinnausfall und Bestandsüberschüsse rufen Lagerkosten hervor.
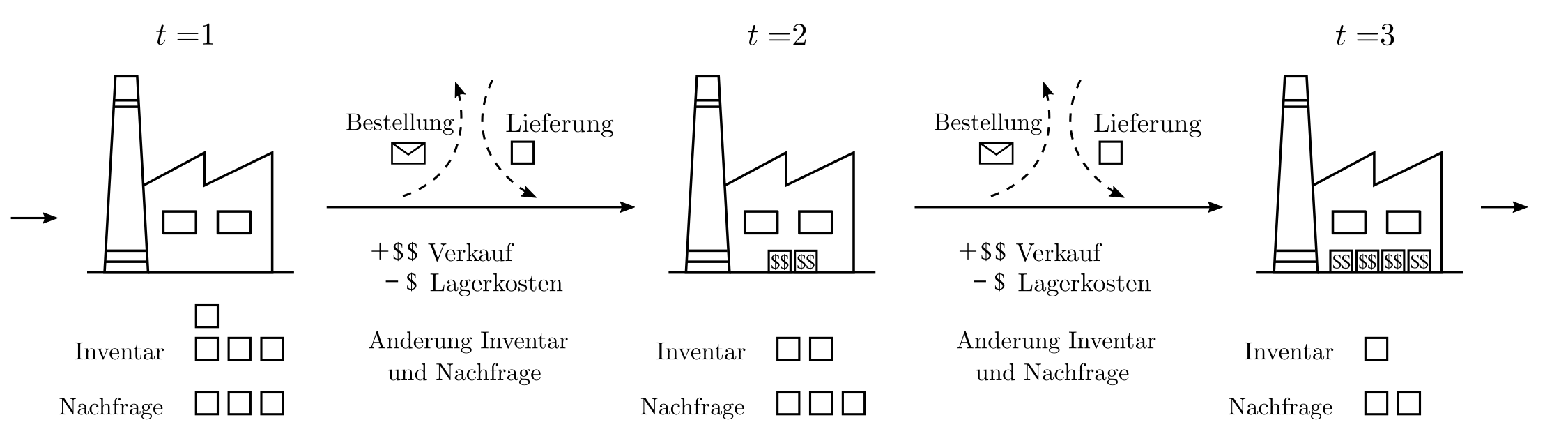
In dem obigen Beispiel ist klar, dass eine konstante Nachorderrate suboptimal ist und Entscheidungen über die Bestellmengen von den jetzigen Beständen, der Nachfrage, und erwarteten Veränderungen beider Parameter abhängen. Eine Formulierung des gesamten Sachverhaltes als einzelne Funktion \(f\) scheint schwierig und tatsächlich wird das Geschehen am besten als Markov-Decision-Process (MDP) dargestellt.
MDP
Ein Markov-Decision-Process (MDP) ist ein steuerbarer stochastischer Prozess. Er besteht aus einem 4‑Tupel \(\{S,A,P,R\}\), welches die Dynamik des Prozesses festlegt.
- \(S\) Eine Menge von Zuständen \(s\)
- \(A\) Eine Menge von Aktionen \(a\)
- \(P(s’| s, a)\) Transitionswahrscheinlichkeiten von \(s\) nach \(s’\) wenn Aktion \(a\) gewählt wird.
- \(R(s’| s, a)\) Die Belohnung bei einer Transition von \(s\) nach \(s’\) via Aktion \(a\).
Es handelt sich demnach um eine Menge von Zuständen \(s\) eines Systems, das sich unter Einfluss von Aktionen \(a\) weiterentwickelt. Dabei ist der Folgezustand \(s’\) abhängig von \(s, a \) , und dem Zufall, die Belohnung von \(s’, s, a\). Ziel ist die Maximierung kumulativer Belohnung. Dazu muss für jeden Zustand die optimale Aktion ermittelt werden. Die Funktion \(\pi:s\mapsto a\) heisst auch policy.
Anwendung Beispiel
Im Kontext des Bestandsplanungsbeispieles ist \(S=\mathbb{R}^2\) da der Zustand durch die zwei Zahlen Bestand und Nachfrage charakterisiert ist. Weiterhin gilt \(A=\mathbb{R}, R(s’, s, a)\) ist die Bilanz aus Verkaufsgewinn und Lagerhaltungskosten, und die Transitionswahrscheinlichkeiten reflektieren \(\text{Bestand}’=\text{Bestand}-\text{Nachfrage}+a\) sowie einen zufälligen Shift der Nachfrage.
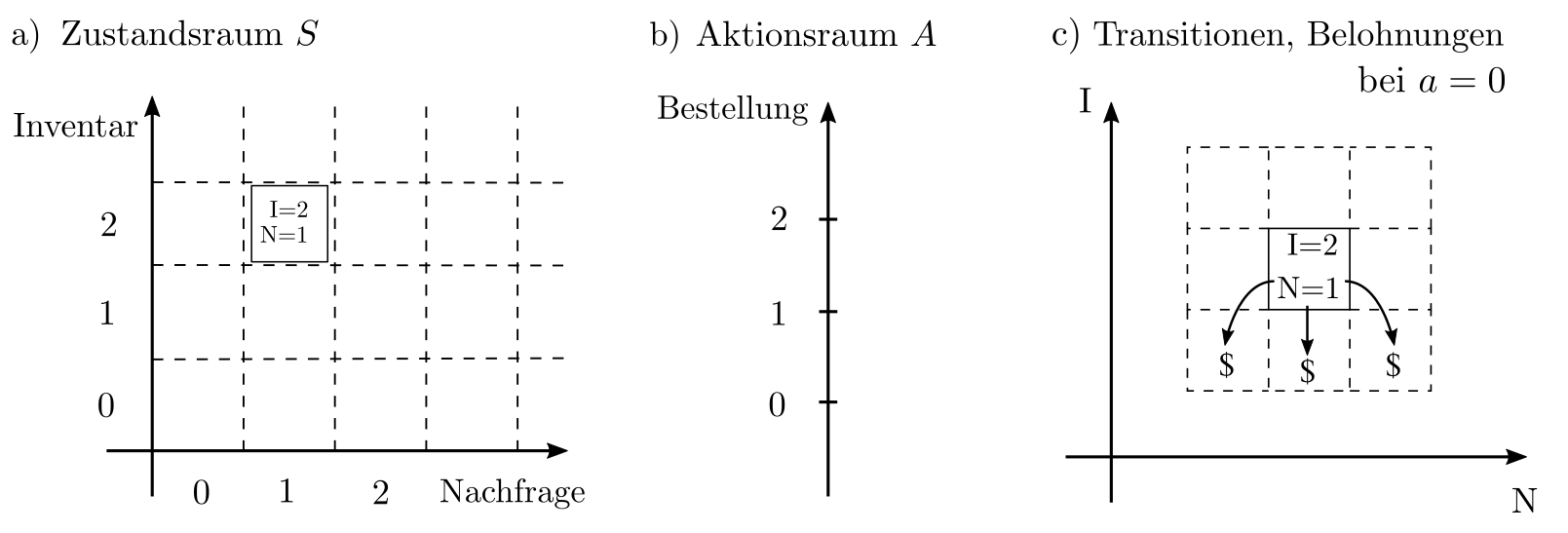
Das Resultat vo DP ist die Policy \(\pi:s\mapsto a\), welche Zustände \(s=(B, N)\) auf die Produktnachbestellungen \(a\) abbildet. Es handelt sich in diesem Fall um eine skalares feld mit Inputdimension 2 (die Zustände) und Outputdimension 1 (die Aktionen).
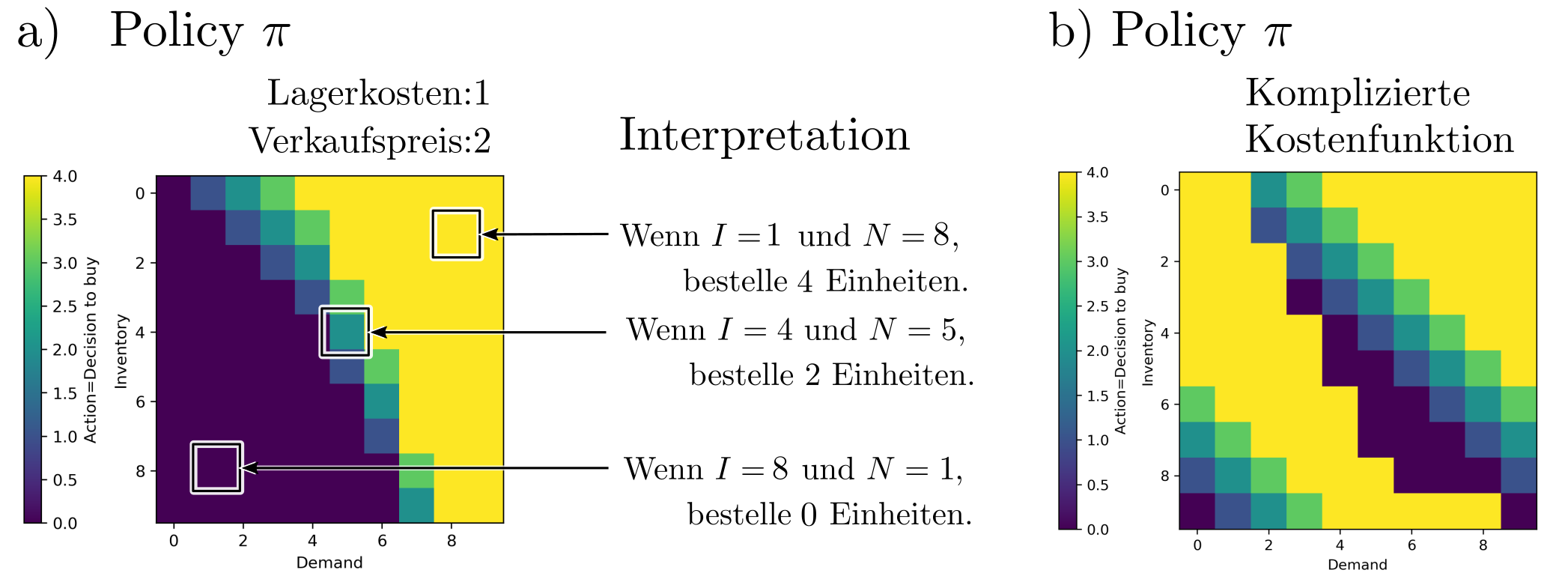
Eine so generierte Policy kann nun in der Praxis benutzt werden, um für jede Konfiguration von Bestand und Nachfrage die erfolgversprechendstend Aktionen zu ermitteln. Damit ist eine Policy mehr als nur ein starrer Plan — sie ist ein adaptiver Massnahmenkatalog.
Anwendungen
DP insbesondere im Zusammenhang mit MDP wird vor allem für die optimale Systemsteuerung verwendet. Selbst in seiner simpelsten Form ist der Formalismus in der Lage, nichtlineare Belohnungen, diskrete Steuerungssignale, und komplizierte Transitionswahrscheinlichkeiten zu handhaben und in optimale Policies umzuwandeln. Die Besonderheit and Policies besteht darin, dass sie flexible Aktionspläne sind, die für alle möglichen Zustände Aktionsketten vorschlagen und somit auch auf unvorhergesehene Ereignisse angemessen und ohne zusätzlichen Aufwand reagieren können.
Planungen mit anderen Methoden wie die Produktionsplanung mit LP liefern nur eine einzelne Abfolge optimaler Entscheidungen ausgehend von einem Anfangszustand und bieten weniger Flexibilität und Adaptivität. Daher wird DP oft im operativen Bereich eingesetzt, wo Entscheidungen schnell getroffen werden müssen und Daten zur probabilistischen Modellierung vorhanden sind. Dies ist der Fall z.B. bei der dynamischen Steuerung von Ampeln, Ambulanzeinsätzen, Kommunikationsnetzwerken, supply chains, und Wasserhaushaltsprozessen, und reicht weiterhin von der prädiktiven Terminplanung in der Medizin, der Belegungsplanung in Callcentern, bis hin zur Entwicklung von Fischereirichtlinien. Details sind hier zu finden.
Lösungsverfahren
In einfachen Fällen, charakterisiert durch endlich viele Zustände und überschaubar viele diskrete Aktionen, können MDP durch interative Verfahren gelöst werden. Um den Term
$$E_{\pi}\left[ \sum_{k=1}^{\text{end}} r(s_{k+1}, s_k, \pi(s_k))\right] $$
repräsentierend die erwartete Gesamtbelohnung zu maximieren, wird typischerweise eine Funktion \(V_{\pi}(s)\) eingeführt. Diese sogenannte Valuefunction misst die erwartete Gesamtbelohnung, wenn startend von Zustand \(s\) aus die Policy \(\pi\) verfolgt wird. Für beliebige Zustände \(s\) und \(s’\) stehen \(V_{\pi}(s)\) und \(V_{\pi}(s’)\) funktional miteinander in Beziehung. Alternierende Iteration zur Bestimmung von \(V_{\pi}\) und zur Optimierung von \(\pi\) wird Valueiteration genannt [1, p. 37] und führt zur optimalen Policy \(\pi^*\).
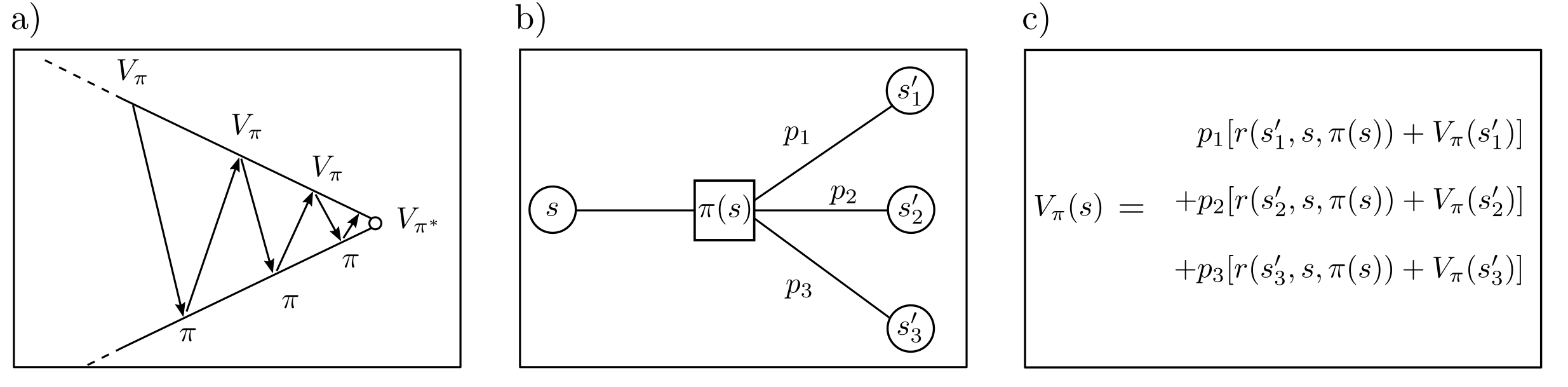
DP für MDP’s in unendlichdimensionalen Räumen ist ebenfalls möglich und wird benötigt, sobald mehr als endlich viele potentielle Zustände oder Aktionen berücksichtigt werden müssen. Dazu werden Folgen linearer Programme gelöst [1, p. 377]. Sind Zustände nur teilweise beobachtbar oder ist das Modell der Zustandsänderungen in Gänze unbekannt, dann sind Formulierungen als Partially observable Markov-decision-process (POMDP) oder als Reinforcement learning Problem möglich.
Praktisches
DP und MDP sind effektiv lösbar mit open source Algorithmen wie z.B. bereitgestellt in der pymdp Toolbox für Python. Die Algorithmen sind jedoch weniger intensiv getestet und gewartet verglichen mit den Algorithmen verfügbar für LP, QP, etc. Die Lösung optimaler Steuerungsprobleme via DP und MDP hat eher experimentellen Charakter. Trotzdem ist es oft der einzige Lösungsansatz, welcher der Komplexität von Echtweltproblemen gerecht wird [2, p. x]. Sowohl die Modellierung des Problemes via Formalisierung der Zustandsräume und Transitionsmatrizen als auch die effektive Lösung von MDP’s sind herausfordernd.
Code & Quellen
Beispielcode: Methods_mdp.py in unserem Tutorialfolder
[1] Feinberg, E. A., and Shwartz, A. (2012). Handbook of Markov Decision Processes: Methods and Applications. Berlin Heidelberg: Springer Science & Business Media.
[2] Boucherie, R. J., & Dijk, N. M. (2017). Markov Decision Processes in Practice. Heidelberg, New York, Dordrecht, London: Springer International Publishing.
[3] Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction. Cambridge: MIT Press.
